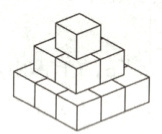
1. 李强同学用棱长为1的正方体在桌面上堆成如图所示的图形,然后把露出的表面都染成红色,则表面被他染成红色的面积为(
A.37
B.33
C.24
D.21
B
)
A.37
B.33
C.24
D.21
答案:
B
2. 两个完全相同的长方体的长、宽、高分别是5 cm、4 cm、3 cm,把它们叠放在一起组成一个新的长方体,在这些新的长方体中,表面积最大是
164
$\mathrm{cm}^2$.
答案:
164
3. 一个棱柱有12个面,那么它的棱数是
30
.
答案:
30
4. 推理猜测题:
(1) 三棱锥有
(2)
(3)
(4) 一个多面体的棱数是8,则这个多面体的面数是
(1) 三棱锥有
6
条棱,四棱锥有8
条棱,十棱锥有20
条棱;(2)
15
棱锥有30条棱;(3)
20
棱柱有60条棱;(4) 一个多面体的棱数是8,则这个多面体的面数是
5
.
答案:
6,8,20,15,20,5
5. 如图,若将类似于①②③④四个图的图形称为平面图,则其顶点数、边数与区域数之间存在某种关系.观察图②和表中对应的数值,探究计数的方法并作答.

(1) 数一数每个图中各有多少个顶点、多少条边,这些边围出多少个区域并填表:
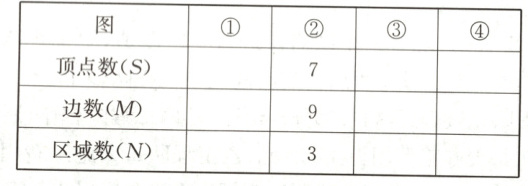
(2) 根据表中数值,写出平面图的顶点数、边数、区域数之间的一种关系;
(3) 如果一个平面图有20个顶点和11个区域,那么利用(2)中得出的关系可知这个平面图有

(1) 数一数每个图中各有多少个顶点、多少条边,这些边围出多少个区域并填表:

(2) 根据表中数值,写出平面图的顶点数、边数、区域数之间的一种关系;
(3) 如果一个平面图有20个顶点和11个区域,那么利用(2)中得出的关系可知这个平面图有
30
条边.
答案:
(1)
| 图 | ① | ② | ③ | ④ |
| --- | --- | --- | --- | --- |
| 顶点数($S$) | 4 | 7 | 8 | 10 |
| 边数($M$) | 6 | 9 | 12 | 15 |
| 区域数($N$) | 3 | 3 | 5 | 6 |
(2) $S + N - M = 1$
(3) 30
(1)
| 图 | ① | ② | ③ | ④ |
| --- | --- | --- | --- | --- |
| 顶点数($S$) | 4 | 7 | 8 | 10 |
| 边数($M$) | 6 | 9 | 12 | 15 |
| 区域数($N$) | 3 | 3 | 5 | 6 |
(2) $S + N - M = 1$
(3) 30
查看更多完整答案,请扫码查看


