1. 如图,已知正方形 $ABCD$ 边长为 $4$,甲、乙两动点分别从顶点 $A$,$C$ 同时出发沿正方形的边开始运动,甲点按顺时针方向运动,乙点按逆时针方向运动,若乙的速度是甲的速度的 $3$ 倍,则它们第 $2022$ 次相遇将在边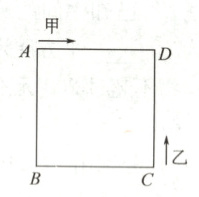
BC
上. 
答案:
BC
2. 某同学在做一套数学试卷时,如果每小时做 $5$ 道题,恰好可以在预定的时间完成. 当他做完 $10$ 道题后,后续解题的效率提高了 $60\%$,不但提前 $3$ 小时完成,而且还多做了其他试卷中的 $6$ 道题. 请根据以上信息,求原试卷中一共有多少道题?
答案:
设原试卷中一共有$ x $道题。
预定完成时间为$ \frac{x}{5} $小时。
做完10道题所用时间:$ \frac{10}{5}=2 $小时。
效率提高60%后,每小时做题数:$ 5×(1+60\%)=8 $道。
实际做题总数为$ x+6 $道,后续做题数:$ (x+6)-10=x-4 $道。
后续做题时间:$ \frac{x-4}{8} $小时。
实际总时间:$ 2+\frac{x-4}{8} $小时。
根据提前3小时完成,可列方程:$ \frac{x}{5}-\left(2+\frac{x-4}{8}\right)=3 $。
解方程:
$\begin{aligned}\frac{x}{5}-2-\frac{x-4}{8}&=3\\8x - 80 - 5(x - 4)&=120\\8x - 80 -5x +20&=120\\3x -60&=120\\3x&=180\\x&=60\end{aligned}$
答:原试卷中一共有$ 60 $道题。
预定完成时间为$ \frac{x}{5} $小时。
做完10道题所用时间:$ \frac{10}{5}=2 $小时。
效率提高60%后,每小时做题数:$ 5×(1+60\%)=8 $道。
实际做题总数为$ x+6 $道,后续做题数:$ (x+6)-10=x-4 $道。
后续做题时间:$ \frac{x-4}{8} $小时。
实际总时间:$ 2+\frac{x-4}{8} $小时。
根据提前3小时完成,可列方程:$ \frac{x}{5}-\left(2+\frac{x-4}{8}\right)=3 $。
解方程:
$\begin{aligned}\frac{x}{5}-2-\frac{x-4}{8}&=3\\8x - 80 - 5(x - 4)&=120\\8x - 80 -5x +20&=120\\3x -60&=120\\3x&=180\\x&=60\end{aligned}$
答:原试卷中一共有$ 60 $道题。
3. 《算法统宗》是中国古代重要的数学著作,其中记载:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空,其大意为:今有若干人住店,若每间住 $7$ 人,则余下 $7$ 人无房可住;若每间住 $9$ 人,则余下一间无人住,求店中共有多少间房?
答案:
设店中共有$x$间房。
根据题意,若每间住$7$人,总人数为$7x + 7$;若每间住$9$人,住人的房间数为$x - 1$,总人数为$9(x - 1)$。
因为总人数不变,所以可列方程:$7x + 7 = 9(x - 1)$
解方程:
$7x + 7 = 9x - 9$
$7 + 9 = 9x - 7x$
$16 = 2x$
$x = 8$
答:店中共有$8$间房。
根据题意,若每间住$7$人,总人数为$7x + 7$;若每间住$9$人,住人的房间数为$x - 1$,总人数为$9(x - 1)$。
因为总人数不变,所以可列方程:$7x + 7 = 9(x - 1)$
解方程:
$7x + 7 = 9x - 9$
$7 + 9 = 9x - 7x$
$16 = 2x$
$x = 8$
答:店中共有$8$间房。
4. 在甲、乙、丙三个容器内分别装有浓度为 $10\%$ 的糖水 $50$ 克、$100$ 克、$150$ 克,现将某种浓度的糖水 $50$ 克倒入甲中,完全混合后,再从甲种取出 $50$ 克倒入乙中,完全混合后,再从乙中取出 $50$ 克倒入丙中,完全混合后发现丙的糖水浓度 $10.5\%$,求最早倒入甲容器中的糖水的浓度.
答案:
设最早倒入甲容器中的糖水浓度为$ x $(小数形式)。
1. 倒入甲容器后:
甲原有溶质:$ 50 × 10\% = 5 $克,倒入溶质:$ 50x $克。
甲溶质总量:$ 5 + 50x $克,溶液总量:$ 50 + 50 = 100 $克。
甲浓度:$ \frac{5 + 50x}{100} $。
2. 从甲取50克倒入乙后:
取出溶质:$ 50 × \frac{5 + 50x}{100} = \frac{5 + 50x}{2} $克。
乙原有溶质:$ 100 × 10\% = 10 $克,乙溶质总量:$ 10 + \frac{5 + 50x}{2} $克,溶液总量:$ 100 + 50 = 150 $克。
乙浓度:$ \frac{10 + \frac{5 + 50x}{2}}{150} $。
3. 从乙取50克倒入丙后:
取出溶质:$ 50 × \frac{10 + \frac{5 + 50x}{2}}{150} = \frac{10 + \frac{5 + 50x}{2}}{3} $克。
丙原有溶质:$ 150 × 10\% = 15 $克,丙溶质总量:$ 15 + \frac{10 + \frac{5 + 50x}{2}}{3} $克,溶液总量:$ 150 + 50 = 200 $克。
4. 丙浓度方程:
丙浓度为$ 10.5\% $,即溶质总量$ 200 × 10.5\% = 21 $克。
列方程:$ 15 + \frac{10 + \frac{5 + 50x}{2}}{3} = 21 $。
5. 解方程:
$\begin{aligned}\frac{10 + \frac{5 + 50x}{2}}{3} &= 6 \\10 + \frac{5 + 50x}{2} &= 18 \\frac{5 + 50x}{2} &= 8 \\5 + 50x &= 16 \\50x &= 11 \\x &= 0.22\end{aligned}$
6. 结果:$ x = 0.22 = 22\% $。
答:最早倒入甲容器中的糖水浓度为$ 22\% $。
1. 倒入甲容器后:
甲原有溶质:$ 50 × 10\% = 5 $克,倒入溶质:$ 50x $克。
甲溶质总量:$ 5 + 50x $克,溶液总量:$ 50 + 50 = 100 $克。
甲浓度:$ \frac{5 + 50x}{100} $。
2. 从甲取50克倒入乙后:
取出溶质:$ 50 × \frac{5 + 50x}{100} = \frac{5 + 50x}{2} $克。
乙原有溶质:$ 100 × 10\% = 10 $克,乙溶质总量:$ 10 + \frac{5 + 50x}{2} $克,溶液总量:$ 100 + 50 = 150 $克。
乙浓度:$ \frac{10 + \frac{5 + 50x}{2}}{150} $。
3. 从乙取50克倒入丙后:
取出溶质:$ 50 × \frac{10 + \frac{5 + 50x}{2}}{150} = \frac{10 + \frac{5 + 50x}{2}}{3} $克。
丙原有溶质:$ 150 × 10\% = 15 $克,丙溶质总量:$ 15 + \frac{10 + \frac{5 + 50x}{2}}{3} $克,溶液总量:$ 150 + 50 = 200 $克。
4. 丙浓度方程:
丙浓度为$ 10.5\% $,即溶质总量$ 200 × 10.5\% = 21 $克。
列方程:$ 15 + \frac{10 + \frac{5 + 50x}{2}}{3} = 21 $。
5. 解方程:
$\begin{aligned}\frac{10 + \frac{5 + 50x}{2}}{3} &= 6 \\10 + \frac{5 + 50x}{2} &= 18 \\frac{5 + 50x}{2} &= 8 \\5 + 50x &= 16 \\50x &= 11 \\x &= 0.22\end{aligned}$
6. 结果:$ x = 0.22 = 22\% $。
答:最早倒入甲容器中的糖水浓度为$ 22\% $。
查看更多完整答案,请扫码查看


