2025年天利38套对接高考单元专题测试卷高中数学选择性必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年天利38套对接高考单元专题测试卷高中数学选择性必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
8. 【新定义】数学中“凸数”是指位数不低于3的奇位数,且最中间的数位上的数字比两边的数字都大的数,则没有重复数字且大于564的三位数中“凸数”的个数为(
A.147
B.112
C.65
D.50
C
)A.147
B.112
C.65
D.50
答案:
8.C【解析】分类加法计数原理 大于564,最高位上的数字是5且没有重复数字的位数为3的“凸数”,中间数位上的数字可以为7,8,9,则共有6+7+8=21(个);大于564,最高位上的数字是6且没有重复数字的位数为3的“凸数”,中间数位上的数字可以为7,8,9,则共有6+7+8=21(个);大于564,最高位上的数字是7且没有重复数字的位数为3的“凸数”,中间数位上的数字可以为8,9,则共有7+8=15(个);大于564,最高位上的数字是8且没有重复数字的位数为3的“凸数”,中间数位上的数字为9,则共有8个,所以没有重复数字且大于564的三位数中“凸数”的个数为21+21+15+8=65.故选C.
9. 某植物园举行花卉展览,某花卉种植园有2种兰花,2种三角梅,共4种精品花卉,其中“绿水晶”是培育的兰花新品种,4种精品花卉将全部去A,B展馆参展,每种只能去一个展馆,每个展馆至少有1种花卉参展,下列选项正确的是(
A.若A展馆需要3种花卉,有4种安排方法
B.若“绿水晶”去A展馆,有7种安排方法
C.若“绿水晶”不去A展馆,有6种安排方法
D.若2种三角梅不能去往同一个展馆,有8种安排方法
ABD
)A.若A展馆需要3种花卉,有4种安排方法
B.若“绿水晶”去A展馆,有7种安排方法
C.若“绿水晶”不去A展馆,有6种安排方法
D.若2种三角梅不能去往同一个展馆,有8种安排方法
答案:
9.ABD【解析】计数原理 对于A,若A展馆需要3种花卉,4种精品花卉选3种安排在A展馆即可,有$C_4^3=4($种)安排方法,故A正确;对于B,若“绿水晶”去A展馆,将剩下3种花卉分别分到A,B展馆即可,B展馆至少有一种,则有$C_3^1+C_3^2+C_3^3=7($种)安排方法,故B正确;对于C,若“绿水晶”不去A展馆,则其必须去B展馆,与B选项同理,有7种安排方法,故C错误;对于D,若2种三角梅不能去往同一个展馆,则其分别在A,B两个展馆,有$A_2^2=2($种)安排方法,将2种兰花安排在A,B两个展馆,每种兰花都有2种安排方法,则2种兰花共有2×2=4(种)安排方法,共有2×4=8(种)安排方法,故D正确.故选ABD.
10. 【数学文化】我国南宋数学家杨辉1261年所著的《详解九章算法》给出了著名的杨辉三角,由此可见我国古代数学的成就是非常值得中华民族自豪的。以下关于杨辉三角的猜想中正确的有(
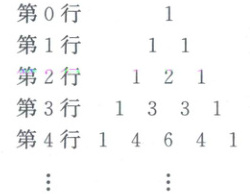
A.第7行中从左到右第5个数与第6个数的比为$5:2$
B.由“第$n$行所有数之和为2的指数幂”猜想:$C_n^0 + C_n^1 + C_n^2 + ·s + C_n^n = 2^n$
C.$C_2^2 + C_3^2 + C_4^2 + C_5^2 + ·s + C_{12}^2 = 286$
D.由“在相邻的两行中,除1以外的每一个数都等于它‘肩上’两个数的和”猜想:$C_{n + 1}^r = C_n^{r - 1} + C_n^r$
BCD
)
A.第7行中从左到右第5个数与第6个数的比为$5:2$
B.由“第$n$行所有数之和为2的指数幂”猜想:$C_n^0 + C_n^1 + C_n^2 + ·s + C_n^n = 2^n$
C.$C_2^2 + C_3^2 + C_4^2 + C_5^2 + ·s + C_{12}^2 = 286$
D.由“在相邻的两行中,除1以外的每一个数都等于它‘肩上’两个数的和”猜想:$C_{n + 1}^r = C_n^{r - 1} + C_n^r$
答案:
10.BCD【解析】杨辉三角的应用 对于A,第7行中从左到右第5个数与第6个数的比为$C_7^4:C_7^5=5:3,$故A不正确;对于B,由二项式系数的性质知$C_n^0+C_n^1+C_n^2+⋯+C_n^n=2^n$成立,故B正确;对于C,$C_6^2+C_6^3+C_6^4+⋯+C_6^12=C_6^2+C_6^3+C_6^4+⋯+C_6^12=C_7^3+C_7^4+⋯+C_7^12=C_8^4=286,$故C正确;对于D,$C_{n - 1}^r+C_n^r=\frac{n!}{(r - 1)!(n - r + 1)!}+\frac{n!}{r!(n - r)!}=\frac{r·n!+(n + 1 - r)·n!}{r!(n + 1 - r)!}=\frac{(n + 1)!}{r!(n + 1 - r)!}=C_{n + 1}^r,$故D正确.故选BCD.
11. 已知集合$M = \{0,1,2,3,4,5\}$。下列说法正确的是(
A.从集合$M$中任取4个元素能够组成300个没有重复数字的四位数
B.从集合$M$中任取3个元素能够组成52个没有重复数字的三位偶数
C.从集合$M$任取3个元素能够组成90个三位密码
D.从集合$M$中任取3个元素,其和是3的倍数的取法共有7种
AB
)A.从集合$M$中任取4个元素能够组成300个没有重复数字的四位数
B.从集合$M$中任取3个元素能够组成52个没有重复数字的三位偶数
C.从集合$M$任取3个元素能够组成90个三位密码
D.从集合$M$中任取3个元素,其和是3的倍数的取法共有7种
答案:
11.AB【解析】计数原理 对于A,从集合M中任取4个元素组成没有重复数字的四位数,若取0,则可以组成$C_8^3C_3^1A_3^3=180($个)(提醒:当选取0时,注意0不能排在首位),若不取0,则可以组成$C_8^4A_4^4=120($个),共180+120=300(个),故A正确;对于B,因为集合M中共有3个偶数,若末位为0,则可以组成$A_5^3=20($个);若末位为2或4,则可以组成$C_2^1C_4^1C_4^1=32($个),所以共有20+32=52(个)(方法:在排数问题中,对于特殊位置特殊元素优先考虑,比如偶数、奇数,可考虑末位数字的特点,还有零不能排首位等).故B正确;对于C,从集合M中任取3个元素能够组成$A_5^3=120($个)三位密码,故C不正确;对于D,从集合M中取3个元素,三个数的和为3的有0,1,2,共1种;三个数的和为6的有0,1,5;1,2,3;0,2,4,共3种;三个数的和为9的有0,4,5;1,3,5;2,3,4,共3种;三个数的和为12的有3,4,5,共1种,则共有1+3+3+1=8(种),故D不正确.综上所述,故选AB.
12. 某年级在一次跨年晚会活动中,有6个不同任务需要安排3名同学完成,每名同学都至少安排一个任务,则不同的安排方法共有
540
种。
答案:
12.540【解析】排列与组合 解决这个问题需分三步完成:第一步把6个任务分成“1+1+4”“1+2+3”“2+2+2”三组;第二步把分好的3组任务分给3名同学(方法:先分组再分配);第三步计算共有$(\frac{C_6^1C_5^1C_4^4}{A_2^2}+\frac{C_6^1C_5^2C_3^3}{A_2^2}+\frac{C_6^2C_4^2C_2^2}{A_3^3})A_3^3=540($种),故不同的安排方法共540种.
13. (2024·新课标Ⅱ卷)在如图的$4×4$的方格表中选4个方格,要求每行和每列均恰有一个方格被选中,则共有
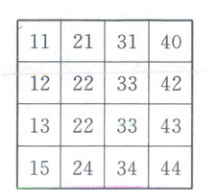
|
24
种选法。在所有符合上述要求的选法中,选中方格中的4个数之和的最大值是112
。
|
答案:
13.24 112【解析】分步乘法计数原理
【思维导图】分别确定在第一、二、三、四行各选1格且不同列的选法数→分步乘法计数原理→计算符合条件的选法数;每一列中十位上的数字都相同→简化方格表→每行最大的数→每行应取的数→原方格表每列应取的数→相加得解.
第一行选1格,共有4种选法;第二行选1格,不可与第一行的同列,共有3种选法;第三行选1格,不可与第一、二行的同列,共有2种选法;第四行选1格,不可与第一、二、三行的同列,只有1种选法,则共有4×3×2×1=24(种)选法满足要求.观察表格可发现,每一列数中十位上的数字都相同,故只考虑个位上的数字即可,简化方格表如
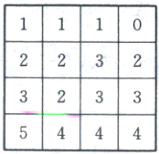
观察可知,第一行最大的数为1,第二行最大的数为3,第三行最大的数为3,第四行最大的数为5,综上,当原方格表第一、二、三、四列分别取15,21,33,43时,所选4个数之和最大,最大值为15+21+33+43=112.
13.24 112【解析】分步乘法计数原理
【思维导图】分别确定在第一、二、三、四行各选1格且不同列的选法数→分步乘法计数原理→计算符合条件的选法数;每一列中十位上的数字都相同→简化方格表→每行最大的数→每行应取的数→原方格表每列应取的数→相加得解.
第一行选1格,共有4种选法;第二行选1格,不可与第一行的同列,共有3种选法;第三行选1格,不可与第一、二行的同列,共有2种选法;第四行选1格,不可与第一、二、三行的同列,只有1种选法,则共有4×3×2×1=24(种)选法满足要求.观察表格可发现,每一列数中十位上的数字都相同,故只考虑个位上的数字即可,简化方格表如

观察可知,第一行最大的数为1,第二行最大的数为3,第三行最大的数为3,第四行最大的数为5,综上,当原方格表第一、二、三、四列分别取15,21,33,43时,所选4个数之和最大,最大值为15+21+33+43=112.
查看更多完整答案,请扫码查看


