2025年天利38套对接高考单元专题测试卷高中数学选择性必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年天利38套对接高考单元专题测试卷高中数学选择性必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
8. 某兴趣小组,对高三刚结束的测试的物理成绩进行随机调查,在所有选择物理科的考生中随机抽取 $100$ 名各类考生的物理成绩,整理数据如下表(单位:人).
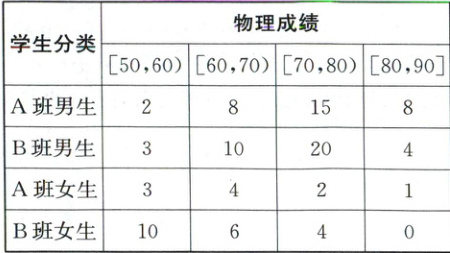
(1)估计该校高三学习物理男生人数与女生人数的比值.
(2)求 A 班物理平均成绩的估计值(同一组中的数据用该组区间中点值为代表,结果四舍五人到整数).
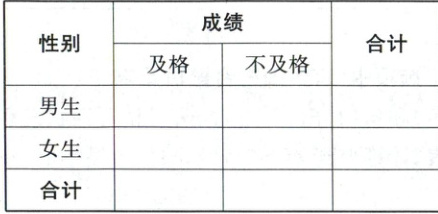
(3)把成绩在 $[60,90]$ 称为及格,成绩在 $[50,60)$ 为不及格,根据所有数据完成下面 $2× 2$ 列联表,试根据小概率值 $\alpha =0.01$ 的独立性检验,分析该校考生的物理成绩与性别是否有关?
附: $\chi ^{2}=\frac {n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$ ,其中 $n=a+b+c+d$ .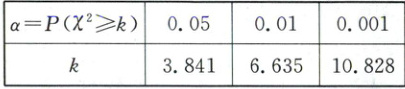

(1)估计该校高三学习物理男生人数与女生人数的比值.
(2)求 A 班物理平均成绩的估计值(同一组中的数据用该组区间中点值为代表,结果四舍五人到整数).
(3)把成绩在 $[60,90]$ 称为及格,成绩在 $[50,60)$ 为不及格,根据所有数据完成下面 $2× 2$ 列联表,试根据小概率值 $\alpha =0.01$ 的独立性检验,分析该校考生的物理成绩与性别是否有关?

附: $\chi ^{2}=\frac {n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$ ,其中 $n=a+b+c+d$ .

答案:
8.平均数+独立性检验
解:
(1)由题表中数据可知,男生共有$2 + 8 + 15 + 8 + 3 + 10 + 20 + 4 = 70$(人),女生共有$3 + 4 + 2 + 1 + 10 + 6 + 4 + 0 = 30$(人)。
由此估计该校高三学习物理男生人数与女生人数的比值约为$\frac{7}{3}$。
(2)A班共有$2 + 3 + 8 + 4 + 15 + 2 + 8 + 1 = 43$(人)。
A班物理平均成绩的估计值为$55 × \frac{5}{43} + 65 × \frac{12}{43} + 75 × \frac{17}{43} + 85 × \frac{9}{43} = \frac{275 + 780 + 1275 + 765}{43} \approx 72$(提示:加权平均数的计算公式)。
(3)补全$2 × 2$列联表如下所示。
| 性别 | 及格 | 不及格 | 合计 |
| --- | --- | --- | --- |
| 男生 | 65 | 5 | 70 |
| 女生 | 17 | 13 | 30 |
| 合计 | 82 | 18 | 100 |
零假设为$H_{0}$:该校考生的物理成绩与性别无关,根据表格中数据计算得到$\chi^{2} = \frac{100 × (65 × 13 - 5 × 17)^{2}}{70 × 30 × 82 × 18} \approx 18.635 > 6.635 = x_{0.01}$(题眼)。
根据小概率值$\alpha = 0.01$的独立性检验,推断$H_{0}$不成立,即认为该校考生的物理成绩与性别有关,此推断犯错误的概率不大于$0.01$。
解:
(1)由题表中数据可知,男生共有$2 + 8 + 15 + 8 + 3 + 10 + 20 + 4 = 70$(人),女生共有$3 + 4 + 2 + 1 + 10 + 6 + 4 + 0 = 30$(人)。
由此估计该校高三学习物理男生人数与女生人数的比值约为$\frac{7}{3}$。
(2)A班共有$2 + 3 + 8 + 4 + 15 + 2 + 8 + 1 = 43$(人)。
A班物理平均成绩的估计值为$55 × \frac{5}{43} + 65 × \frac{12}{43} + 75 × \frac{17}{43} + 85 × \frac{9}{43} = \frac{275 + 780 + 1275 + 765}{43} \approx 72$(提示:加权平均数的计算公式)。
(3)补全$2 × 2$列联表如下所示。
| 性别 | 及格 | 不及格 | 合计 |
| --- | --- | --- | --- |
| 男生 | 65 | 5 | 70 |
| 女生 | 17 | 13 | 30 |
| 合计 | 82 | 18 | 100 |
零假设为$H_{0}$:该校考生的物理成绩与性别无关,根据表格中数据计算得到$\chi^{2} = \frac{100 × (65 × 13 - 5 × 17)^{2}}{70 × 30 × 82 × 18} \approx 18.635 > 6.635 = x_{0.01}$(题眼)。
根据小概率值$\alpha = 0.01$的独立性检验,推断$H_{0}$不成立,即认为该校考生的物理成绩与性别有关,此推断犯错误的概率不大于$0.01$。
查看更多完整答案,请扫码查看


