《2025年天利38套对接高考单元专题测试卷高中数学选择性必修第二册人教版》

1. 若经验回归方程中的回归系数$\hat{b}=0$时，则相关系数为(C)

A.$r = 1$
B.$r = -1$
C.$r = 0$
D.无法确定

答案： 1.C 【解析】相关系数 $x$ 的值不随 $y$ 的值变化而变化，
相关不密切，相关系数为0，故选C.

2. 在建立两个变量$y$与$x$的回归模型时，分别选择了 4 个不同的模型，模型 1，2，3，4 的决定系数$R^{2}$依次为 0.20，0.48，0.96，0.85，则其中拟合效果最好的模型是(B)

A.模型 4
B.模型 3
C.模型 2
D.模型 1

答案： 2.B 【解析】回归模型 因为 $R^2$ 越大，表示残差平方和
越小，即模型的拟合效果越好，所以在这4个不同的模
型中，拟合效果最好的模型是模型3.故选B.

3. 下列随机事件中的随机变量$X$服从超几何分布的是(C)

A.将一枚硬币连抛 3 次，记正面向上的次数为$X$
B.某射手的射击命中率为 0.8，现对目标射击 1 次，记命中的次数为$X$
C.从 7 男 3 女共 10 名学生干部中选出 5 名学生干部，记选出女生的人数为$X$
D.盒中有 4 个白球和 3 个黑球，每次从中摸出 1 个球且不放回，记第一次摸出黑球时摸取的次数为$X$

答案： 3.C 【解析】超几何分布 对于A，将一枚硬币连抛3次，
记正面向上的次数为 $X$，则 $X$ 服从二项分布，故A不满
足题意;对于B，某射手的射击命中率为0.8，现对目标
射击1次，记命中的次数为 $X$，则 $X$ 服从两点分布，故
B不满足题意;对于C，从7男3女共10名学生干部中
选出5名学生干部，记选出女生的人数为 $X$，则 $X$ 服从
超几何分布，故C满足题意;对于D，盒中有4个白球和
3个黑球，每次从中摸出1个球且不放回，记第一次摸出
黑球时摸取的次数为 $X$，则 $X$ 不服从超几何分布，故
D不满足题意.故选C.

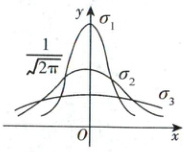
4. 如图是当$\sigma$取三个不同值$\sigma_{1},\sigma_{2},\sigma_{3}$的三种正态曲线$N(0,\sigma^{2})$的图象，那么$\sigma_{1},\sigma_{2},\sigma_{3}$的大小关系是(D)


A.$\sigma_{1}＞1＞\sigma_{2}＞\sigma_{3}＞0$
B.$0＜\sigma_{1}＜\sigma_{2}＜1＜\sigma_{3}$
C.$\sigma_{1}＜\sigma_{2}＞1＞\sigma_{3}＞0$
D.$0＜\sigma_{1}＜\sigma_{2}=1＜\sigma_{3}$

答案： 4.D 【解析】正态曲线 当 $\mu=0,\sigma=1$ 时，正态曲线
$f(x)=\frac {1}{\sqrt {2\pi}}e^{-\frac {x^2}{2}}$.在 $x=0$ 时，取最大值 $\frac {1}{\sqrt {2\pi}}$.故 $\sigma_2=$
1.由正态曲线的特征知，当 $\mu$ 一定时，曲线的形状由 $\sigma$
确定. $\sigma$ 越小，曲线越“瘦高”; $\sigma$ 越大，曲线越“矮胖”.于
有 $0＜\sigma_1＜\sigma_2=1＜\sigma_3$.故选D.

5. 某商场有 a，b 两种抽奖活动，a，b 两种抽奖活动中奖的概率分别为$\frac{2}{5},\frac{3}{5}$，每人只能参加其中一种抽奖活动. 甲参加 a，b 两种抽奖活动的概率分别为$\frac{2}{5},\frac{3}{5}$，已知甲中奖，则甲参加 a 抽奖活动中奖的概率为(D)

A.$\frac{9}{25}$
B.$\frac{4}{25}$
C.$\frac{9}{13}$
D.$\frac{4}{13}$

答案： 5.D 【解析】全概率公式+条件概率公式 用事件 $A_1$，
$A_2$ 分别表示甲参加 $a,b$ 两种抽奖活动，B 表示甲中奖，
则 $P(A_1)=\frac {2}{5},P(A_2)=\frac {3}{5},P(B|A_1)=\frac {2}{5},P(B|A_2)=$
$\frac {3}{5}$,由全概率公式得 $P(B)=P(A_1)P(B|A_1)+P(A_2)·$
$P(B|A_2)=\frac {2}{5}× \frac {2}{5}+\frac {3}{5}× \frac {3}{5}=\frac {13}{25}$,所以甲参加 $a$ 抽奖活
动中奖的概率 $P(A_1|B)=\frac {P(A_1B)}{P(B)}=\frac {P(B|A_1)P(A_1)}{P(B)}=$
$\frac {4}{13}$.故选D.

6. 为了研究某产品的年研发费用$x$(单位：万元)与年利润$y$(单位：万元)的关系，该公司统计了最近 8 年每年投入该产品的年研发费用与年利润的数据，根据统计数据的散点图可以看出$y$与$x$之间有线性相关关系，设其回归直线方程为$\hat{y}=\hat{b}x+\hat{a}$. 已知$\sum_{i = 1}^{8}x_{i}=80,\sum_{i = 1}^{8}y_{i}=200,\hat{b}=2$. 若该公司对该产品预投入的年研发费用为 25 万元，则预测年利润为(A)

A.55 万元
B.57 万元
C.60 万元
D.62 万元

答案： 6.A 【解析】一元线性回归模型及其应用 $\because \sum_{i=1}^{8}x_i=80$,
$\sum_{i=1}^{8}y_i=200,\therefore \bar{x}=\frac {\sum_{i=1}^{8}x_i}{8}=10,\bar{y}=\frac {\sum_{i=1}^{8}y_i}{8}=25.\therefore \hat{a}=$
$\bar{y}-\hat{b}\bar{x}=25 - 2×10=5.\therefore y$ 关于 $x$ 的回归直线方程为
$\hat{y}=2x+5.\therefore$ 当 $x=25$ 时,$\hat{y}=2×25+5=55$(万元).故
选A.