《2025年天利38套对接高考单元专题测试卷高中数学选择性必修第二册人教版》

12. 某同学参加学校数学知识竞赛，规定每个同学答 20 道题，已知该同学每道题答对的概率为 0.6，每道题答对与否相互独立. 若答对一题得 3 分，答错一题扣 1 分，则该同学总得分的数学期望为28，方差为76.8.

答案： 12.28 76.8 【解析】随机变量的数学期望与方差 设该
同学答对题目的数量为 $\xi$,因为该同学每道题答对的概
率为0.6，共答20道题，所以 $\xi\sim B(20,0.6)$.所以
$E(\xi)=20×0.6=12$,$D(\xi)=20×0.6×(1-0.6)=$
4.8.设该同学总得分为 $\eta$，则 $\eta=3\xi-(20-\xi)=4\xi-$
20,则 $E(\eta)=4E(\xi)-20=28$,$D(\eta)=16D(\xi)=4.8×$
16=76.8.

13. 现有甲、乙两个口袋，其中甲口袋内装有三个 1 号球，两个 2 号球和一个 3 号球；乙口袋内装有两个 1 号球，一个 2 号球，一个 3 号球. 第一次从甲口袋中任取 1 个球，将取出的球放入乙口袋中，第二次从乙口袋中任取一个球，则第二次取到 2 号球的概率为$\frac {4}{15}$.

答案： 13.$\frac {4}{15}$ 【解析】随机事件的概率+全概率公式 由题意，
记事件 $A_i,B_i$ 分别表示第一次、第二次取到 $i$ 号球，
$i=1,2,3$，由题意 $A_1,A_2,A_3$ 两两互斥(题眼)，其和为
$\Omega$，并且 $P(A_1)=\frac {3}{6}=\frac {1}{2},P(A_2)=\frac {2}{6}=\frac {1}{3},P(A_3)=\frac {1}{6},\therefore P(B_2|A_1)=\frac {1}{5},P(B_2|A_2)=\frac {2}{5},P(B_2|A_3)=$
$\frac {1}{6}.\therefore P(B_2)=\sum_{i=1}^{3}P(A_i)P(B_2|A_i)=\frac {1}{2}×\frac {1}{5}+\frac {1}{3}×$
$\frac {2}{5}+\frac {1}{6}×\frac {1}{5}=\frac {4}{15}$(题眼)(提示：全概率公式).

14. 有甲、乙两个班级共计 105 人进行数学考试，按照大于等于 85 分为优秀，85 分以下为非优秀统计成绩，得到如下所示的列联表.

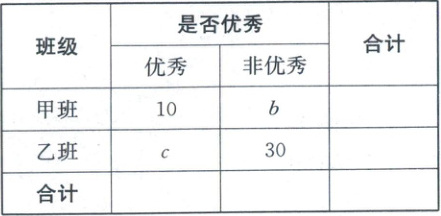
附：$\chi^{2}=\frac{n(ad - bc)^{2}}{(a + b)(c + d)(a + c)(b + d)}$，其中$n = a + b + c + d$.

已知在全部 105 人中随机抽取 1 人，成绩优秀的概率为$\frac{2}{7}$，则下列说法正确的是②③.
①列联表中$c$的值为 30，$b$的值为 35；
②列联表中$c$的值为 20，$b$的值为 45；
③根据列联表中的数据，若按 95%的可靠性要求，能认为“成绩与班级有关系”；
④根据列联表中的数据，若按 95%的可靠性要求，不能认为“成绩与班级有关系”.

答案： 14.②③ 【解析】独立性检验 因为在105人中随机抽取
1人，成绩优秀的概率为 $\frac {2}{7}$，所以成绩优秀的人数为
$105×\frac {2}{7}=30$，非优秀人数为 $105-30=75$，所以 $c=$
$30-10=20$,$b=75-30=45$，故①错误，②正确;因为
$\chi^2\approx6.109＞3.841=x_{0.05}$，所以按95%的可靠性要求，
能认为“成绩与班级有关系”.故③正确，④错误.综上，
说法正确的是②③.

15. (13 分)一个池塘里的鱼的数目记为$N$，从池塘里捞出 200 尾鱼，并给鱼作上标识，然后把鱼放回池塘里，过一小段时间后再从池塘里捞出 500 尾鱼，$X$表示捞出的 500 尾鱼中有标识的鱼的数目.
(1) 若$N = 5000$，求$X$的数学期望.
(2) 已知捞出的 500 尾鱼中 15 尾有标识，试给出$N$的估计值（以使得$P(X = 15)$最大的$N$的值作为$N$的估计值）.

答案： 15.超几何分布的概率+数学期望
【思维导图】
(1)已知条件$\rightarrow X$ 服从超几何分布$\rightarrow$
$E(X)$.
(2)已知条件$\rightarrow\begin{cases} N＜685\rightarrow P(X=15)=0;\\N\geq685\rightarrow P(X=15)\end{cases}$
记 $a(N)=\frac {\mathrm{C}_{200}^{15}\mathrm{C}_{N-200}^{485}}{\mathrm{C}_{N}^{500}}$(题眼)，
则$\frac {a(N+1)}{a(N)}=\frac {\mathrm{C}_{N+1}^{500}\mathrm{C}_{N-200}^{485}}{\mathrm{C}_{N+1-200}^{485}\mathrm{C}_{N}^{500}}=$
$\frac {(N+1-500)(N+1-200-485)}{(N+1)(N-485)}=$
$\frac {(N-499)(N-199)}{(N+1)(N-684)}$
令 $N^2-698N+499×199＞N^2-683N-684$，
解得 $N＜\frac {499×199+684}{15}\approx6665.7$，
故当 $685\leq N\leq6665$ 时,$a(N+1)＞a(N)$;
当 $N\geq6666$ 时,$a(N+1)＜a(N)$，
故 $N=6666$ 时,$a(N)$最大，
所以 $N$ 的估计值为6666.
(13分)