2025年天利38套对接高考单元专题测试卷高中数学选择性必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年天利38套对接高考单元专题测试卷高中数学选择性必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1.【跨学科】如图,只闭合两个开关将一条电路从 A 处到 B 处接通,可构成线路的条数为(
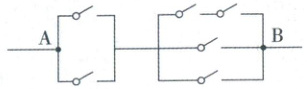
A.8
B.4
C.5
D.3
B
)
A.8
B.4
C.5
D.3
答案:
1.B 【解析】分步乘法计数原理 根据分步计数原理,一条电路从A处到B处接通,A处并联电路开关闭合一个,有2种方法,B处并联电路开关若只闭合一个,只能闭合下面两个中的一个,有2种方法,共有$2 × 2 = 4$(种)方法.故选B.
2. 若 $ C_{n}^{1}x + C_{n}^{2}x^{2} + ·s + C_{n}^{n}x^{n} $ 能被 5 整除,则 $ x,n $ 的一组值可能为(
A.$ x = 2,n = 6 $
B.$ x = 4,n = 6 $
C.$ x = 8,n = 4 $
D.$ x = 14,n = 4 $
C
)A.$ x = 2,n = 6 $
B.$ x = 4,n = 6 $
C.$ x = 8,n = 4 $
D.$ x = 14,n = 4 $
答案:
2.C 【解析】二项式定理 已知$C_{n}x + C_{n}^{2}x^{2} + C_{n}^{3}x^{3} + ·s + C_{n}^{n}x^{n} = (1 + x)^{n} - 1$.当$x = 2,n = 6$时,原式$= 3^{6} - 1 = (3^{3} + 1)(3^{3} - 1) = 28 × 26$,不能被5整除;当$x = 4,n = 6$时,原式$= 5^{6} - 1$,不能被5整除;当$x = 8,n = 4$时,原式$= 9^{4} - 1 = (9^{2} + 1)(9^{2} - 1) = 82 × 80$,能被5整除;当$x = 14,n = 4$时,原式$= 15^{4} - 1 = (15^{2} + 1)(15^{2} - 1) = 226 × 224$,不能被5整除,故选C.
3. 预制菜指以各类农、畜、禽、水产品为原辅料,配以调味料等辅料经预选、调制等工艺加工而成的半成品.近几年预制菜市场规模快速增长,某城市调查近 4 个月的预制菜市场规模 $ y $(元)得到如表所示的数据,根据数据得到 $ y $ 关于 $ x $ 的非线性回归方程 $ \hat{y} = e^{\frac{x}{5} - a} $.
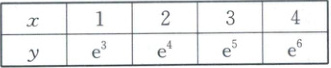
按照这样的速度,预估第 6 个月的预制菜市场规模是(
A.$ e^{8} $ 万元
B.$ e^{7} $ 万元
C.$ e^{\frac{9}{2}} $ 万元
D.$ e^{\frac{11}{2}} $ 万元

按照这样的速度,预估第 6 个月的预制菜市场规模是(
D
)A.$ e^{8} $ 万元
B.$ e^{7} $ 万元
C.$ e^{\frac{9}{2}} $ 万元
D.$ e^{\frac{11}{2}} $ 万元
答案:
3.D 【解析】非线性回归方程+预测值 令$z = \ln y$,则$z = \frac{x}{5} - a$,可得$z$关于$x$的数据如下表,所以$\bar{x} = \frac{1}{4} × (1 + 2 + 3 + 4) = \frac{5}{2}$,$\bar{z} = \frac{1}{4} × (3 + 4 + 5 + 6) = \frac{9}{2}$.又$(\bar{x},\bar{z})$的坐标必满足回归方程$z = \frac{x}{5} - a$,所以$\frac{9}{2} = \frac{1}{5} × \frac{5}{2} - a$,解得$a = - 4$,所以$\hat{y} = e^{\frac{x}{5} + 4}$.当$x = 6$时,$\hat{y} = e^{\frac{6}{5} + 4} = e^{\frac{26}{5}}$,即预估第6个月的预制菜市场规模是$e^{\frac{26}{5}}$万元.故选D.
|x|1|2|3|4|
|----|----|----|----|----|
|z|3|4|5|6|
|x|1|2|3|4|
|----|----|----|----|----|
|z|3|4|5|6|
4. 若 $ (2x - 1)^{4} = a_{4}x^{4} + a_{3}x^{3} + a_{2}x^{2} + a_{1}x + a_{0} $,则 $ a_{0} + a_{2} + a_{4} = $(
A.-40
B.41
C.-41
D.82
B
)A.-40
B.41
C.-41
D.82
答案:
4.B 【解析】二项展开式 设$f(x) = (2x - 1)^{4} = a_{4}x^{4} + a_{3}x^{3} + a_{2}x^{2} + a_{1}x + a_{0}$,则$f(1) = 1 = a_{4} + a_{3} + a_{2} + a_{1} + a_{0}$,$f( - 1) = 3^{4} = a_{4} - a_{3} + a_{2} - a_{1} + a_{0}$,所以$a_{0} + a_{2} + a_{4} = \frac{f(1) + f( - 1)}{2} = \frac{1 + 3^{4}}{2} = 41$.故选B.
5. 青少年的身高一直是家长和社会关注的重点,它不仅关乎个体成长,也是社会健康素养发展水平的体现. 某市教育部门为了了解本市高三学生的身高状况,从本市全体高三学生中随机抽查了 1 200 人,经统计后发现样本的身高(单位:cm)近似服从正态分布 $ N(172,\sigma^{2}) $,且身高在 168 cm 到 176 cm 之间的人数占样本量的 75%,则样本中身高不低于 176 cm 的约有(
A.150 人
B.300 人
C.600 人
D.900 人
A
)A.150 人
B.300 人
C.600 人
D.900 人
答案:
5.A 【解析】正态分布的应用 由$N(172,\sigma^{2})$知,该正态分布曲线关于直线$x = 172$对称(题眼),所以$P(168 < X < 176) = 2P(172 < X < 176) = 0.75$.所以$P(172 < X < 176) = 0.375$.所以$P(X \geqslant 176) = 0.5 - P(172 < X < 176) = 0.5 - 0.375 = 0.125$.所以样本中身高不低于176cm的约有$0.125 × 1200 = 150$(人).故选A.
6. 某篮球队在对球员的使用上总是进行数据分析,根据以往的数据统计,甲球员能够胜任大前锋、小前锋、组织后卫以及得分后卫四个位置,且出场率分别为 0.2,0.5,0.2,0.1,当甲球员担当大前锋、小前锋、组织后卫以及得分后卫时,球队输球的概率依次为 0.4,0.2,0.6,0.2. 当甲球员参加比赛时,该球队某场比赛不输球的概率为(
A.0.3
B.0.32
C.0.68
D.0.7
C
)A.0.3
B.0.32
C.0.68
D.0.7
答案:
6.C 【解析】全概率公式+对立事件的概率公式 设$A_{1}$表示“甲球员担当大前锋”,$A_{2}$表示“甲球员担当小前锋”,$A_{3}$表示“甲球员担当组织后卫”,$A_{4}$表示“甲球员担当得分后卫”,$B$表示“当甲球员参加比赛时,球队输球”.根据题意,则$P(B) = P(A_{1})P(B|A_{1}) + P(A_{2})P(B|A_{2}) + P(A_{3})P(B|A_{3}) + P(A_{4})P(B|A_{4}) = 0.2 × 0.4 + 0.5 × 0.2 + 0.2 × 0.6 + 0.1 × 0.2 = 0.32$,所以当甲球员参加比赛时,该球队某场比赛不输球的概率为$1 - 0.32 = 0.68$.故选C.
7. 将 a,b,c,d,e 五名实习教师分配到某校高二年级的甲、乙、丙 3 个班级实习,要求每个班至少一名,最多两名,其中 a 不去甲班,则不同的分配方案有(
A.180 种
B.150 种
C.90 种
D.60 种
D
)A.180 种
B.150 种
C.90 种
D.60 种
答案:
7.D 【解析】计数原理 根据题意,去甲班实习的教师可以是1人或2人.当有1人去甲班时,因为a不去甲班,所以从另外4人中选1人去甲班,有$C_{4}^{1}$种选法,再选2人去乙班,有$C_{3}^{2}$种选法,剩下2人去丙班,有$C_{2}^{2}$种选法,分3步完成,共有$C_{4}^{1}C_{3}^{2}C_{2}^{2} = 4 × 6 × 1 = 24$(种)方案;当有2人去甲班时,因为a不去甲班,所以从另外4人中选2人去甲班,有$C_{4}^{2}$种选法,剩余3人分配到2个班的分法有$C_{3}^{2}A_{2}^{2}$种方法,故共有$C_{4}^{2}C_{3}^{2}A_{2}^{2} = 6 × 3 × 2 = 36$(种),所以不同的分配方案共有$24 + 36 = 60$(种).故选D.
查看更多完整答案,请扫码查看


