2025年天利38套对接高考单元专题测试卷高中数学选择性必修第一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年天利38套对接高考单元专题测试卷高中数学选择性必修第一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 如图,在平行六面体 $ABCD - A'B'C'D'$ 中,以各顶点为起点和终点的向量中,与 $\overrightarrow{AA'}$ 一定相等的向量有 (
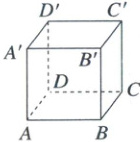
A.3个
B.4个
C.5个
D.6个
A
)
A.3个
B.4个
C.5个
D.6个
答案:
1.A【解析】相等向量 由题图可知,与$\overrightarrow{AA^{\prime}}$相等的向量有$\overrightarrow{BB^{\prime}},\overrightarrow{CC^{\prime}},\overrightarrow{DD^{\prime}}$,共$3$个,故选A
2. 若直线 $l$ 的方向向量与平面 $\alpha$ 的法向量的夹角等于 $110^{\circ}$,则直线 $l$ 与平面 $\alpha$ 所成的角等于 (
A.$20^{\circ}$
B.$70^{\circ}$
C.$110^{\circ}$
D.以上均错
A
)A.$20^{\circ}$
B.$70^{\circ}$
C.$110^{\circ}$
D.以上均错
答案:
2.A【解析】平面的法向量+直线与平面所成的角 因为直线$l$的方向向量与平面$\alpha$的法向量的夹角等于$110^{\circ}$,所以直线$l$与平面$\alpha$所成的角为$110^{\circ}-90^{\circ}=20^{\circ}$.故选A.
3. 若两个不同平面 $\alpha,\beta$ 的一个法向量分别为 $\boldsymbol{u}=(1,2,-1),\boldsymbol{v}=(2,3,8)$,则 (
A.$\alpha//\beta$
B.$\alpha\perp\beta$
C.$\alpha,\beta$ 相交但不垂直
D.以上均不正确
B
)A.$\alpha//\beta$
B.$\alpha\perp\beta$
C.$\alpha,\beta$ 相交但不垂直
D.以上均不正确
答案:
3.B【解析】面面垂直的充要条件 由题可知$\boldsymbol{u}·\boldsymbol{v}=(1,2,-1)·(2,3,8)=0$,所以$\boldsymbol{u}\perp\boldsymbol{v}$,即$\alpha\perp\beta$.故选B
4. 设 $A,B,C,D$ 是半径为 1 的球 $O$ 的球面上的四个点. 设 $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\boldsymbol{0}$,则 $|AD| + |BD| + |CD|$ 不可能等于 (
A.3
B.$\frac{7}{2}$
C.4
D.$3\sqrt{2}$
A
)A.3
B.$\frac{7}{2}$
C.4
D.$3\sqrt{2}$
答案:
4.A【解析】空间向量的运算 $\because\overrightarrow{AD}+\overrightarrow{BD}+\overrightarrow{CD}=\overrightarrow{OD}-\overrightarrow{OA}+\overrightarrow{OD}-\overrightarrow{OB}+\overrightarrow{OD}-\overrightarrow{OC}=3\overrightarrow{OD}-(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})=3\overrightarrow{OD}$,$\therefore|\overrightarrow{AD}+\overrightarrow{BD}+\overrightarrow{CD}|=3|\overrightarrow{OD}|=3$.$\because|\overrightarrow{AD}|+|\overrightarrow{BD}|+|\overrightarrow{CD}|\geqslant|\overrightarrow{AD}+\overrightarrow{BD}+\overrightarrow{CD}|$,当且仅当$\overrightarrow{AD},\overrightarrow{BD},\overrightarrow{CD}$同向时,等号成立,而A,B,C,D在球面上,不可能共线,即$\overrightarrow{AD},\overrightarrow{BD},\overrightarrow{CD}$不同向,$\therefore|\overrightarrow{AD}|+|\overrightarrow{BD}|+|\overrightarrow{CD}|>|\overrightarrow{AD}+\overrightarrow{BD}+\overrightarrow{CD}|=3$,且$|\overrightarrow{AD}|+|\overrightarrow{BD}|+|\overrightarrow{CD}|<6$.综上,$3<|\overrightarrow{AD}|+|\overrightarrow{BD}|+|\overrightarrow{CD}|<6$,故选A
5. 如图所示,在棱长为 1 的正方体 $ABCD - A_1B_1C_1D_1$ 中,点 $P$ 为截面 $A_1C_1B$ 上的动点,若 $DP\perp A_1C$,则点 $P$ 的轨迹长度是 (
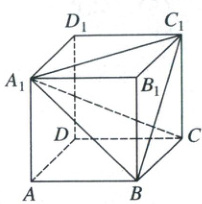
A.$\frac{\sqrt{2}}{2}$
B.$\sqrt{2}$
C.$\frac{1}{2}$
D.1
B
)
A.$\frac{\sqrt{2}}{2}$
B.$\sqrt{2}$
C.$\frac{1}{2}$
D.1
答案:
5.B【解析】立体几何中的动点轨迹问题 以$D$为坐标原点建立如图所示空间直角坐标系,因为正方体棱长为$1$,所以$D(0,0,0),A_{1}(1,0,1),B(1,1,0),C(0,1,0),C_{1}(0,1,1)$.所以$\overrightarrow{A_{1}C_{1}}=(-1,1,0),\overrightarrow{A_{1}B}=(0,1,-1),\overrightarrow{A_{1}C}=(-1,1,-1)$.因为点$P$在平面$A_{1}C_{1}B$上,所以设$\overrightarrow{A_{1}P}=m\overrightarrow{A_{1}C_{1}}+n\overrightarrow{A_{1}B}=(-m,m+n,-n)$(题眼),$P(x,y,z)$.则$\overrightarrow{A_{1}P}=(x-1,y,z-1)$,所以$x=1-m$,$y=m+n$,$z=1-n$.所以$P(1-m,m+n,1-n)$.所以$\overrightarrow{DP}=(1-m,m+n,1-n)$.因为$DP\perp A_{1}C$,所以$\overrightarrow{DP}·\overrightarrow{A_{1}C}=m-1+m+n+n-1=0$,即$m+n=1$.所以点$P$在线段$BC_{1}$上.则点$P$的轨迹长度是$BC_{1}=\sqrt{2}$,

5.B【解析】立体几何中的动点轨迹问题 以$D$为坐标原点建立如图所示空间直角坐标系,因为正方体棱长为$1$,所以$D(0,0,0),A_{1}(1,0,1),B(1,1,0),C(0,1,0),C_{1}(0,1,1)$.所以$\overrightarrow{A_{1}C_{1}}=(-1,1,0),\overrightarrow{A_{1}B}=(0,1,-1),\overrightarrow{A_{1}C}=(-1,1,-1)$.因为点$P$在平面$A_{1}C_{1}B$上,所以设$\overrightarrow{A_{1}P}=m\overrightarrow{A_{1}C_{1}}+n\overrightarrow{A_{1}B}=(-m,m+n,-n)$(题眼),$P(x,y,z)$.则$\overrightarrow{A_{1}P}=(x-1,y,z-1)$,所以$x=1-m$,$y=m+n$,$z=1-n$.所以$P(1-m,m+n,1-n)$.所以$\overrightarrow{DP}=(1-m,m+n,1-n)$.因为$DP\perp A_{1}C$,所以$\overrightarrow{DP}·\overrightarrow{A_{1}C}=m-1+m+n+n-1=0$,即$m+n=1$.所以点$P$在线段$BC_{1}$上.则点$P$的轨迹长度是$BC_{1}=\sqrt{2}$,

6. 如图,在棱长为 $2\sqrt{2}$ 的正四面体(四个面都是正三角形)$ABCD$ 中,$E,F$ 分别为 $BC,CD$ 的中点,且 $\overrightarrow{AF}$ 在 $\overrightarrow{DE}$ 方向上的投影向量为 $\lambda\overrightarrow{DE}$,则 $\lambda$ 的值为 (
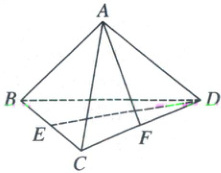
A.$\frac{1}{6}$
B.$-\frac{1}{6}$
C.$\frac{\sqrt{6}}{6}$
D.$-\frac{\sqrt{6}}{6}$
B
)
A.$\frac{1}{6}$
B.$-\frac{1}{6}$
C.$\frac{\sqrt{6}}{6}$
D.$-\frac{\sqrt{6}}{6}$
答案:
6.B【解析】空间向量的坐标运算 如图,将正四面体嵌套在正方体内,并以$A$为坐标原点,建立空间直角坐标系,因为正四面体$ABCD$的棱长为$2\sqrt{2}$,所以正方体的棱长为$2$.则$A(0,0,0),B(2,2,0),C(0,2,2),D(2,0,2),E(1,2,1),F(1,1,2)$,可得$\overrightarrow{AF}=(1,1,2),\overrightarrow{DE}=(-1,2,-1)$,则$\overrightarrow{AF}$在$\overrightarrow{DE}$方向上的投影向量为$\frac{\overrightarrow{AF}·\overrightarrow{DE}}{|\overrightarrow{DE}|^{2}}·\overrightarrow{DE}=\frac{-1}{\sqrt{6}×\sqrt{6}}\overrightarrow{DE}=-\frac{1}{6}\overrightarrow{DE}$,所以$\lambda$的值为$-\frac{1}{6}$.故选B.

6.B【解析】空间向量的坐标运算 如图,将正四面体嵌套在正方体内,并以$A$为坐标原点,建立空间直角坐标系,因为正四面体$ABCD$的棱长为$2\sqrt{2}$,所以正方体的棱长为$2$.则$A(0,0,0),B(2,2,0),C(0,2,2),D(2,0,2),E(1,2,1),F(1,1,2)$,可得$\overrightarrow{AF}=(1,1,2),\overrightarrow{DE}=(-1,2,-1)$,则$\overrightarrow{AF}$在$\overrightarrow{DE}$方向上的投影向量为$\frac{\overrightarrow{AF}·\overrightarrow{DE}}{|\overrightarrow{DE}|^{2}}·\overrightarrow{DE}=\frac{-1}{\sqrt{6}×\sqrt{6}}\overrightarrow{DE}=-\frac{1}{6}\overrightarrow{DE}$,所以$\lambda$的值为$-\frac{1}{6}$.故选B.

7. 在平行六面体 $ABCD - A_1B_1C_1D_1$ 中,$AB = AD = AA_1$,$\angle DAB = \angle BAA_1 = \angle DAA_1 = 60^{\circ}$,$\overrightarrow{A_1Q}=\lambda\overrightarrow{A_1B}(0\lt\lambda\lt1)$,则直线 $AC_1$ 与直线 $DQ$ 所成角的余弦值为 (
A.0
B.$\frac{1}{2}$
C.$\frac{\sqrt{3}}{2}$
D.1
A
)A.0
B.$\frac{1}{2}$
C.$\frac{\sqrt{3}}{2}$
D.1
答案:
7.A【解析】异面直线所成角 如图,设$\boldsymbol{a}=\overrightarrow{AB},\boldsymbol{b}=\overrightarrow{AD},\boldsymbol{c}=\overrightarrow{AA_{1}}$,$\overrightarrow{AB}=\overrightarrow{AD}=\overrightarrow{AA_{1}}=1$,则$\boldsymbol{a}·\boldsymbol{b}=\boldsymbol{a}·\boldsymbol{c}=\boldsymbol{b}·\boldsymbol{c}=\frac{1}{2}$,$\overrightarrow{AC_{1}}=\boldsymbol{a}+\boldsymbol{b}+\boldsymbol{c}$,$\overrightarrow{A_{1}B}=\overrightarrow{AB}-\overrightarrow{AA_{1}}=\boldsymbol{a}-\boldsymbol{c}$,$\overrightarrow{DQ}=\overrightarrow{DD_{1}}+\overrightarrow{D_{1}A_{1}}+\overrightarrow{A_{1}Q}=\boldsymbol{c}-\boldsymbol{b}+\lambda(\boldsymbol{a}-\boldsymbol{c})=\lambda\boldsymbol{a}-\boldsymbol{b}+(1-\lambda)\boldsymbol{c}$,$\overrightarrow{AC_{1}}·\overrightarrow{DQ}=(\boldsymbol{a}+\boldsymbol{b}+\boldsymbol{c})·[\lambda\boldsymbol{a}-\boldsymbol{b}+(1-\lambda)\boldsymbol{c}]=\lambda\boldsymbol{a}^{2}-\boldsymbol{a}·\boldsymbol{b}+(1-\lambda)\boldsymbol{a}·\boldsymbol{c}+\lambda\boldsymbol{a}·\boldsymbol{b}-\boldsymbol{b}^{2}+(1-\lambda)\boldsymbol{b}·\boldsymbol{c}+\lambda\boldsymbol{a}·\boldsymbol{c}-\boldsymbol{b}·\boldsymbol{c}+(1-\lambda)\boldsymbol{c}^{2}=\lambda-\frac{1}{2}-\frac{1}{2}\lambda+\frac{1}{2}\lambda-\frac{1}{2}+\frac{1}{2}\lambda+\frac{1}{2}\lambda-1+\frac{1}{2}-\lambda+1-\lambda=0$(题眼),即$\overrightarrow{AC_{1}}\perp\overrightarrow{DQ}$,所以直线$\overrightarrow{AC_{1}}$与直线$DQ$所成角的余弦值为$0$.故选A

7.A【解析】异面直线所成角 如图,设$\boldsymbol{a}=\overrightarrow{AB},\boldsymbol{b}=\overrightarrow{AD},\boldsymbol{c}=\overrightarrow{AA_{1}}$,$\overrightarrow{AB}=\overrightarrow{AD}=\overrightarrow{AA_{1}}=1$,则$\boldsymbol{a}·\boldsymbol{b}=\boldsymbol{a}·\boldsymbol{c}=\boldsymbol{b}·\boldsymbol{c}=\frac{1}{2}$,$\overrightarrow{AC_{1}}=\boldsymbol{a}+\boldsymbol{b}+\boldsymbol{c}$,$\overrightarrow{A_{1}B}=\overrightarrow{AB}-\overrightarrow{AA_{1}}=\boldsymbol{a}-\boldsymbol{c}$,$\overrightarrow{DQ}=\overrightarrow{DD_{1}}+\overrightarrow{D_{1}A_{1}}+\overrightarrow{A_{1}Q}=\boldsymbol{c}-\boldsymbol{b}+\lambda(\boldsymbol{a}-\boldsymbol{c})=\lambda\boldsymbol{a}-\boldsymbol{b}+(1-\lambda)\boldsymbol{c}$,$\overrightarrow{AC_{1}}·\overrightarrow{DQ}=(\boldsymbol{a}+\boldsymbol{b}+\boldsymbol{c})·[\lambda\boldsymbol{a}-\boldsymbol{b}+(1-\lambda)\boldsymbol{c}]=\lambda\boldsymbol{a}^{2}-\boldsymbol{a}·\boldsymbol{b}+(1-\lambda)\boldsymbol{a}·\boldsymbol{c}+\lambda\boldsymbol{a}·\boldsymbol{b}-\boldsymbol{b}^{2}+(1-\lambda)\boldsymbol{b}·\boldsymbol{c}+\lambda\boldsymbol{a}·\boldsymbol{c}-\boldsymbol{b}·\boldsymbol{c}+(1-\lambda)\boldsymbol{c}^{2}=\lambda-\frac{1}{2}-\frac{1}{2}\lambda+\frac{1}{2}\lambda-\frac{1}{2}+\frac{1}{2}\lambda+\frac{1}{2}\lambda-1+\frac{1}{2}-\lambda+1-\lambda=0$(题眼),即$\overrightarrow{AC_{1}}\perp\overrightarrow{DQ}$,所以直线$\overrightarrow{AC_{1}}$与直线$DQ$所成角的余弦值为$0$.故选A

查看更多完整答案,请扫码查看


