2025年天利38套对接高考单元专题测试卷高中数学选择性必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年天利38套对接高考单元专题测试卷高中数学选择性必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
7. 足球是一项大众喜爱的运动,为了解喜爱足球是否与性别有关,随机抽取了若干人进行调查,抽取的女性人数是男性人数的 2 倍,男性喜爱足球的人数占男性人数的 $ \frac{5}{6} $,女性喜爱足球的人数占女性人数的 $ \frac{1}{3} $,若本次调查得出“在犯错误的概率不超过 0.005 的前提下认为喜爱足球与性别有关”的结论,则被调查的男性至少有(
附:$ \chi^2 = \frac{n(ad - bc)^2}{(a + b)(c + d)(a + c)(b + d)} $,其中 $ n = a + b + c + d $。

A.13 人
B.12 人
C.11 人
D.10 人
B
)附:$ \chi^2 = \frac{n(ad - bc)^2}{(a + b)(c + d)(a + c)(b + d)} $,其中 $ n = a + b + c + d $。

A.13 人
B.12 人
C.11 人
D.10 人
答案:
7.B[解析]独立性检验 设被调查的男性有$x$人,则女性有$2x$人,依据题意可得列联表如下:
|性别|喜好|男性|女性|合计|
|----|----|----|----|----|
| |喜爱足球|$\frac{5x}{6}$|$\frac{2x}{3}$|$\frac{3x}{2}$|
| |不喜爱足球|$\frac{x}{6}$|$\frac{4x}{3}$|$\frac{3x}{2}$|
| |合计|$x$|$2x$|$3x$|
$\chi^{2}=\frac{3x(\frac{5x}{6} · \frac{4x}{3}-\frac{2x}{3} · \frac{x}{6})^{2}}{\frac{3x}{2} · \frac{3x}{2} · x · 2x}=\frac{2x}{3}$。因为本次调查得出“在犯错误的概率不超过0.005的前提下认为喜爱足球与性别有关”的结论,所以有$\chi^{2} \geqslant 7.879$(题眼)。即$\frac{2x}{3} \geqslant 7.879$,解得$x \geqslant 11.8185$。又因为上述列联表中的所有数字均为整数,所以$x$的最小值为12。故选B。
|性别|喜好|男性|女性|合计|
|----|----|----|----|----|
| |喜爱足球|$\frac{5x}{6}$|$\frac{2x}{3}$|$\frac{3x}{2}$|
| |不喜爱足球|$\frac{x}{6}$|$\frac{4x}{3}$|$\frac{3x}{2}$|
| |合计|$x$|$2x$|$3x$|
$\chi^{2}=\frac{3x(\frac{5x}{6} · \frac{4x}{3}-\frac{2x}{3} · \frac{x}{6})^{2}}{\frac{3x}{2} · \frac{3x}{2} · x · 2x}=\frac{2x}{3}$。因为本次调查得出“在犯错误的概率不超过0.005的前提下认为喜爱足球与性别有关”的结论,所以有$\chi^{2} \geqslant 7.879$(题眼)。即$\frac{2x}{3} \geqslant 7.879$,解得$x \geqslant 11.8185$。又因为上述列联表中的所有数字均为整数,所以$x$的最小值为12。故选B。
8. 下列说法不正确的是(
A.一组数据 1,4,14,6,13,10,17,19 的 $ 25\% $ 分位数为 5
B.一组数据 $ m $,3,2,5,7 的中位数为 3,则 $ m $ 的取值范围是 $ (-\infty,3] $
C.若随机变量 $ X \sim B(4,\frac{1}{3}) $,则方差 $ D(3X + 1) = 4 $
D.若随机变量 $ X \sim N(1,\sigma^2) $,且 $ P(0 < X < 1) = 0.4 $,则 $ P(X > 2) = 0.1 $
C
)A.一组数据 1,4,14,6,13,10,17,19 的 $ 25\% $ 分位数为 5
B.一组数据 $ m $,3,2,5,7 的中位数为 3,则 $ m $ 的取值范围是 $ (-\infty,3] $
C.若随机变量 $ X \sim B(4,\frac{1}{3}) $,则方差 $ D(3X + 1) = 4 $
D.若随机变量 $ X \sim N(1,\sigma^2) $,且 $ P(0 < X < 1) = 0.4 $,则 $ P(X > 2) = 0.1 $
答案:
8.C[解析]百分位数+中位数+方差+正态分布 对于A,该组数据共8个,且$8 × 25\% = 2$,所以25%分位数为从小到大排列后第2个数和第3个数的平均数,即为$\frac{4 + 6}{2} = 5$,故A正确。对于B,若$m \geqslant 5$,则这组数据由小到大排列为2,3,5,m,7或2,3,5,7,m,中位数为5,不符合题意;若$3 < m < 5$,则这组数据由小到大排列为2,3,m,5,7或2,3,5,7,m,中位数为m ≠ 3,不符合题意;若$m \leqslant 3$,则这组数据由小到大排列为2,m,3,5,7或m,2,3,5,7,中位数为3,故实数m的取值范围是$(-\infty,3]$,故B正确。对于C,若随机变量$X \sim B(4,\frac{1}{3})$,则$D(X)=4 × \frac{1}{3} × (1 - \frac{1}{3})=\frac{8}{9}$,所以$D(3X + 1)=3^{2}D(X)=9 × \frac{8}{9}=8$。故C错误。对于D,若随机变量$X \sim N(1,\sigma^{2})$,且$P(0 < X < 1)=0.4$,则$P(X > 2)=0.5 - P(1 < X < 2)=0.5 - P(0 < X < 1)=0.1$,故D正确。故选C。
9. 自然环境中,大气压受到各种因素的影响,如温度、湿度、风速和海拔等方面的改变,都将导致大气压发生相应的变化,其中以海拔的影响最为显著。如图是根据一组观测数据得到海拔 6 km~15 km 的大气压强散点图,根据一元线性回归模型得到回归直线方程为 $ y_1 = -4.0x + 68.5 $,决定系数为 $ R_1^2 = 0.99 $;根据非线性回归模型得到回归方程为 $ y_2 = 132.9e^{-0.163x} $,决定系数为 $ R_2^2 = 0.99 $,则下列说法正确的是(
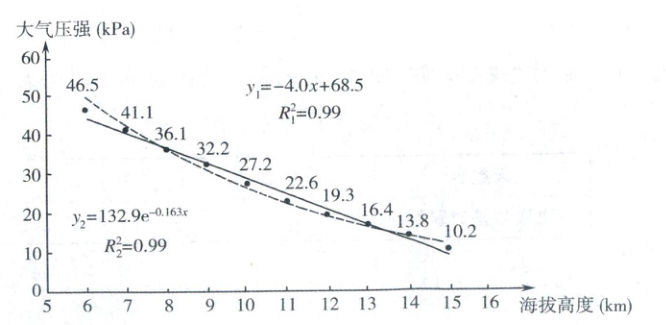
A.由散点图可知,大气压强与海拔高度负相关
B.由方程 $ y_1 = -4.0x + 68.5 $ 可知,海拔每升高 1 km,大气压强必定降低 4.0 kPa
C.由方程 $ y_1 = -4.0x + 68.5 $ 可知,样本点 $ (11,22.6) $ 的残差为 -1.9
D.对比两个回归模型,结合实际情况,方程 $ y_2 = 132.9e^{-0.163x} $ 的预报效果更好
ACD
)
A.由散点图可知,大气压强与海拔高度负相关
B.由方程 $ y_1 = -4.0x + 68.5 $ 可知,海拔每升高 1 km,大气压强必定降低 4.0 kPa
C.由方程 $ y_1 = -4.0x + 68.5 $ 可知,样本点 $ (11,22.6) $ 的残差为 -1.9
D.对比两个回归模型,结合实际情况,方程 $ y_2 = 132.9e^{-0.163x} $ 的预报效果更好
答案:
9.ACD[解析]回归模型的实际应用 对于A,由题知,海拔高度越高,大气压强越小(题眼),所以大气压强与海拔高度负相关,故A正确;对于B,回归直线得到的数据为估计值(题眼),而非精确值,故B错误;对于C,当$x = 11$时,$\hat{y}_{1} = -4.0 × 11 + 68.5 = 24.5$,又由散点图知观测值为22.6(题眼),所以样本点$(11,22.6)$的残差为$22.6 - 24.5 = -1.9$,故C正确;对于D,随着海拔高度的增加,大气压强越来越小,但不可能为负数(题眼),因此方程$y_{2}=132.9e^{-0.163x}$的预报效果更好,故D正确。故选ACD。
查看更多完整答案,请扫码查看


