2025年天利38套对接高考单元专题测试卷高中数学选择性必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年天利38套对接高考单元专题测试卷高中数学选择性必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
21. 将 1 到 10 这 10 个正整数平均分成甲、乙两组,每组 5 个正整数,且甲组的中位数比乙组的中位数小 1,则不同的平分方法共有
36
种.
答案:
21.36【解析】中位数+组合的实际应用 依题意,得甲组的中位数必为5,乙组的中位数必为6,所以甲组另外四个数,可从1,2,3,4和7,8,9,10这两组数中各取2个,共有$C_{4}^{2}C_{4}^{2}=36$(种)平分方法.
22. 【五育并举】第 42 届潍坊国际风筝会期间,某学校派 5 人参加连续 6 天的志愿服务活动,其中甲连续参加 2 天,其他人各参加 1 天,则不同的安排方法有
120
种(结果用数值表示).
答案:
22.120【解析】排列与组合 在6天的志愿服务活动中,甲连续参加2天,共有5种情况,剩下的4人全排列有$A_{4}^{4}$种情况,故不同的安排方法有$5× A_{4}^{4}=120$(种).
23. 为推动黄河流域生态保护和高质量发展,某市环保局派出 4 个宣传小组,到黄河沿岸 5 个社区做环保宣讲活动,每个小组至少去 1 个社区,每个社区只安排 1 个小组,则不同的安排方法共有
240
种(用数字作答).
答案:
23.240【解析】排列组合的实际应用 由题知,有一个小组必去两个社区,把5个社区分成4组有$C_{5}^{2}$种分法,将分成的4组安排给4个宣传小组有$A_{4}^{4}$种方法,所以不同的安排方法共有$C_{5}^{2}A_{4}^{4}=10×24=240$(种).
24. (2023·新课标Ⅰ卷)某学校开设了 4 门体育类选修课和 4 门艺术类选修课,学生需从这 8 门课中选修 2 门或 3 门课,并且每类选修课至少选修 1 门,则不同的选课方案共有
64
种(用数字作答).
答案:
24.64【解析】计数原理
解法一:选课方案可以分成两类:第一类,选修2门,总的方案减去不符合要求的,有$C_{8}^{2}-2C_{2}^{2}=16$(种);第二类,选修3门,有$C_{8}^{3}-2C_{3}^{3}=48$(种).综上,不同的选课方案共有16+48=64(种).
解法二:选课方案可以分成两类:第一类,选修2门,每一类各选1门,有$C_{4}^{1}· C_{4}^{1}=16$(种);第二类,选修3门,一类选1门另一类选2门,有$2· C_{4}^{1}· C_{4}^{2}=48$(种).综上,不同的选课方案共有16+48=64(种).
解法一:选课方案可以分成两类:第一类,选修2门,总的方案减去不符合要求的,有$C_{8}^{2}-2C_{2}^{2}=16$(种);第二类,选修3门,有$C_{8}^{3}-2C_{3}^{3}=48$(种).综上,不同的选课方案共有16+48=64(种).
解法二:选课方案可以分成两类:第一类,选修2门,每一类各选1门,有$C_{4}^{1}· C_{4}^{1}=16$(种);第二类,选修3门,一类选1门另一类选2门,有$2· C_{4}^{1}· C_{4}^{2}=48$(种).综上,不同的选课方案共有16+48=64(种).
25. 我国河流旅游资源非常丰富,夏季到景点漂流是很多家庭的最佳避暑选择. 某家庭共 6 个人,包括 4 个大人,2 个小孩,计划去贵州漂流. 景点现有 3 只不同的船只可供他们选择使用,每船最多可乘 3 人,为了安全起见,小孩必须要大人陪同,则不同的乘船方式共有
348
种.
答案:
25.348【解析】排列组合的应用 ①若6人乘坐3只船,先将4个大人分成2,1,1三组有$C_{4}^{2}=6$(种)方法,然后将三组排到3只船有$A_{3}^{3}=6$(种)方法,再将2个小孩排到3只船有$3×3-1=8$(种)方法,所以共有$6×6×8=288$(种)方法.②若6人乘坐2只船,共有$\frac{C_{6}^{3}}{A_{2}^{2}}× A_{3}^{2}=$60(种)方法(易错:相同个数分组问题注意除以顺序).综上,共有288+60=348(种)方法.
方法技巧
分组分配问题的解题思路一般是先分组再分配
(1)对于整体均分,$n$组元素个数相同,不管它们的顺序如何,分组后一定要除以$A_{n}^{n}$;
(2)对于部分均分,若$m$组元素个数相同,分组后一定要除以$A_{m}^{m}$;
(3)对于不等分组,只需先分组,后排列.
方法技巧
分组分配问题的解题思路一般是先分组再分配
(1)对于整体均分,$n$组元素个数相同,不管它们的顺序如何,分组后一定要除以$A_{n}^{n}$;
(2)对于部分均分,若$m$组元素个数相同,分组后一定要除以$A_{m}^{m}$;
(3)对于不等分组,只需先分组,后排列.
26. (2024·上海卷)设集合 A 中的元素皆为无重复数字的三位正整数,且元素中任意两者之积皆为偶数,求集合中元素个数的最大值为
329
.
答案:
26.329【解析】组合+集合的性质 由偶数$×$偶数=偶数,偶数$×$奇数=偶数,奇数$×$奇数=奇数可知,若集合中任意两个元素的积为偶数,则该集合中最多只能有一个奇数,其余均为偶数.先研究集合中无重复数字的三位正偶数,若个位数为0,这样的偶数有$2× C_{5}^{2}=$72(个)(提示:十位数、百位数不重复);若个位数不为0,这样的偶数有$C_{4}^{1}C_{5}^{1}C_{4}^{1}=256$(个)(提示:个位数可选2,4,6,8,然后百位数从非0和非个位数的剩下8个数中选1个,最后十位数从除个位数与百位数以外的8个数中选1个),所以集合中元素个数的最大值为256+72+1=329(提示:加1指的是加一个奇数).
27. 甲、乙、丙、丁、戊、己六位同学中考语文、数学、外语的成绩如表:
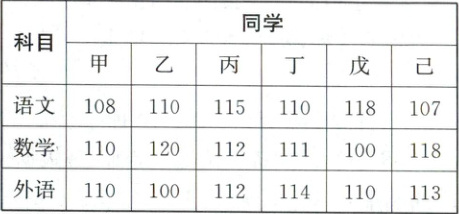
将每人中考成绩最高的科目认定为他的“最擅长科目”,例如甲的最擅长科目为数学和外语. 现从这六位同学中选出三人分别担任语文、数学、外语三个科目的科代表(每科一人,不可兼任),若每个科代表对应的科目都是他的最擅长科目,则符合要求的安排方法共有

将每人中考成绩最高的科目认定为他的“最擅长科目”,例如甲的最擅长科目为数学和外语. 现从这六位同学中选出三人分别担任语文、数学、外语三个科目的科代表(每科一人,不可兼任),若每个科代表对应的科目都是他的最擅长科目,则符合要求的安排方法共有
10
种.
答案:
27.10【解析】排列组合+分类加法计数原理 由题表可知,甲最擅长的科目为数学和外语,乙最擅长的科目为数学,丙最擅长的科目为语文,丁最擅长的科目为外语,戊最擅长的科目为语文,己最擅长的科目为数学,所以语文科代表可从丙、戊两位同学中选择,数学科代表可从甲、乙、己三位同学中选择,外语科代表可从甲、丁两位同学中选择,若甲不为科代表,则只需选语文、数学科代表即可,有$C_{2}^{1}C_{3}^{1}=4$(种)选法;若甲为数学科代表,则只需选语文科代表即可,有$C_{2}^{1}=2$(种)选法;若甲为外语科代表,则只需选语文、数学科代表即可,有$C_{2}^{1}C_{3}^{1}=4$(种)选法.综上所述,共有10种安排方法.
28. 有包括甲、乙在内的 3 名男生和 3 名女生,按照不同的要求站成一排,则
(1)任何两名男生都不相邻的排队方案有多少种.
(2)若 3 名男生的顺序一定,则不同的排队方案有多少种.
(3)甲、乙两名同学之间恰有 2 人的不同排队方案有多少种.
(1)任何两名男生都不相邻的排队方案有多少种.
(2)若 3 名男生的顺序一定,则不同的排队方案有多少种.
(3)甲、乙两名同学之间恰有 2 人的不同排队方案有多少种.
答案:
28.排列组合的应用
解:
(1)先将3名女生全排列,有$A_{3}^{3}$种情况,排好后有4个空位,在4个空位中任选3个,安排3名男生,有$A_{4}^{3}$种情况,则任何两名男生不相邻的排法共有$A_{3}^{3}A_{4}^{3}=$144(种)排队方案.
(2)先在6个位置排3个女生,共$A_{6}^{3}$种排法,3名男生顺序一定,排进余下的三个位置,只有1种情况,则共有$A_{6}^{3}×1=120$(种)排队方案.
(3)从除甲、乙以外的4人中任取2人排在甲、乙之间,与甲、乙组成一个整体,再与余下2个人全排列,共有$C_{4}^{2}A_{2}^{2}A_{2}^{2}A_{3}^{3}=144$(种)排队方案.
解:
(1)先将3名女生全排列,有$A_{3}^{3}$种情况,排好后有4个空位,在4个空位中任选3个,安排3名男生,有$A_{4}^{3}$种情况,则任何两名男生不相邻的排法共有$A_{3}^{3}A_{4}^{3}=$144(种)排队方案.
(2)先在6个位置排3个女生,共$A_{6}^{3}$种排法,3名男生顺序一定,排进余下的三个位置,只有1种情况,则共有$A_{6}^{3}×1=120$(种)排队方案.
(3)从除甲、乙以外的4人中任取2人排在甲、乙之间,与甲、乙组成一个整体,再与余下2个人全排列,共有$C_{4}^{2}A_{2}^{2}A_{2}^{2}A_{3}^{3}=144$(种)排队方案.
查看更多完整答案,请扫码查看


