《2025年天利38套对接高考单元专题测试卷高中数学选择性必修第二册人教版》

15. (13 分)“绿水青山就是金山银山”是习近平总书记于 2005 年 8 月在浙江湖州安吉考察时提出的科学论断。为提高学生环保意识，某校决定在高一、高二年级开展环保知识测试，已知高一、高二年级每个学生通过测试的概率分别为 $ \frac{3}{5} $，$ \frac{2}{3} $。
(1) 从高二年级随机抽取 6 人参加测试，求通过测试的人数不多于 4 人的概率。
(2) 若两个年级各选派部分学生参加测试，高二年级通过测试人数的标准差为 $ \frac{10}{3} $，则高一年级至少选派多少人参加测试，才能使其通过测试人数的均值不低于高二年级。

答案： 15.二项分布+二项分布的均值与方差
解：设高二年级参加测试人数为n，通过测试人数为X，则$X \sim B(n,\frac{2}{3})$（提醒：当X服从二项分布时，应先确定$X \sim B(n,p)$中的试验次数n与成功概率p）。
(1)由题意，n = 6，$\therefore P(X \leqslant 4)=1 - P(X = 5) - P(X = 6)=1 - C_{6}^{5}(\frac{2}{3})^{5}(\frac{1}{3})^{1} - C_{6}^{6}(\frac{2}{3})^{6}(\frac{1}{3})^{0}$（提醒：公式$P(X = k)=C_{n}^{k}p^{k}(1 - p)^{n - k}(k = 0,1,·s,n)$必须在满足“独立重复试验”时才能运用，否则不能应用该公式）$=\frac{473}{729}$。
(2)$D(X)=n · \frac{2}{3}(1 - \frac{2}{3})=\frac{2n}{9}$（提示：如果$X \sim B(n,p)$，则$E(X)=np$，$D(X)=np(1 - p)$）。
$\because \sqrt{D(X)}=\frac{\sqrt{2n}}{3}=\frac{10}{3}$，$\therefore n = 50$（题眼）。
$\therefore E(X)=\frac{100}{3}$。
设高一年级参加测试人数为m，通过测试人数为Y，则$Y \sim B(m,\frac{3}{5})$。
易知$E(Y)=\frac{3m}{5}$，
由题意，$E(Y) \geqslant E(X)$，即$\frac{3m}{5} \geqslant \frac{100}{3}$，
得$m \geqslant \frac{500}{9}=55\frac{5}{9}$，
$\therefore$高一年级至少选派56人参加测试，才能使其通过测试人数的均值不低于高二年级。

16. (15 分)某教育教研机构为了研究学生理科思维和文科思维的差异情况，对某班级 35 名同学的数学成绩和语文成绩进行了统计并整理成如下 $ 2 × 2 $ 列联表（单位：人）：

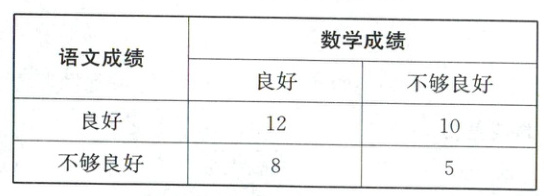
从该班的学生中任选一人，$ A $ 表示事件“选到的学生数学成绩良好”，$ B $ 表示事件“选到的学生语文成绩良好”，$ \frac{P(A|B)}{P(\overline{A}|B)} $ 与 $ \frac{P(A|\overline{B})}{P(\overline{A}|\overline{B})} $ 的比值是文、理科思维差异化的一项度量指标，记该指标为 $ R $。
(1) 证明：$ R = \frac{P(B|A)}{P(\overline{B}|A)} · \frac{P(\overline{B}|\overline{A})}{P(B|\overline{A})} $。
(2) 利用该表中数据，给出 $ P(B|A) $，$ P(B|\overline{A}) $ 的估计值，并利用(1)的结果给出 $ R $ 的估计值。

答案： 16.条件概率
解：
(1)证明：$R=\frac{P(A|B)}{P(A|\bar{B})} · \frac{P(\bar{A}|B)}{P(\bar{A}|\bar{B})}=\frac{\frac{P(AB)}{P(B)} · \frac{P(B)}{P(\bar{A}B)} · \frac{P(\bar{A}B)}{P(\bar{B})} · \frac{P(\bar{B})}{P(\bar{A}\bar{B})}}{\frac{P(A)}{P(B)} · \frac{P(\bar{B})}{P(A\bar{B})} · \frac{P(\bar{A})}{P(\bar{A}B)} · \frac{P(B)}{P(\bar{A})}}=\frac{P(B|A)}{P(\bar{B}|A)} · \frac{P(\bar{B}|\bar{A})}{P(B|\bar{A})}$，得证。
(2)由已知得$P(B|A)=\frac{12}{20}$，$P(\bar{B}|A)=\frac{10}{15}$。
又$P(B|\bar{A})=\frac{8}{20}$，$P(\bar{B}|\bar{A})=\frac{5}{15}$，
所以$R=\frac{P(B|A)}{P(\bar{B}|A)} · \frac{P(\bar{B}|\bar{A})}{P(B|\bar{A})}=\frac{3}{4}$。