2025年天利38套对接高考单元专题测试卷高中数学选择性必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年天利38套对接高考单元专题测试卷高中数学选择性必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 某校乒乓球社团为了了解喜欢乒乓球运动是否与性别有关,随机抽取了若干人进行调查. 已知抽查的男生、女生人数均为 $6m(m\in \mathbf{N}^{*})$ ,其中男生喜爱乒乓球运动的人数占男生人数的 $\frac{2}{3}$ ,女生喜爱乒乓球运动的人数占女生人数的 $\frac{1}{2}$ . 若本次调查得出“有 $99.5\%$ 的把握认为喜爱乒乓球运动与性别有关”的结论,则 $m$ 的最小值为 (
附: $\chi ^{2}=\frac {n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$ ,其中 $n=a+b+c+d$ .

A.$20$
B.$21$
C.$22$
D.$23$
D
)附: $\chi ^{2}=\frac {n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$ ,其中 $n=a+b+c+d$ .

A.$20$
B.$21$
C.$22$
D.$23$
答案:
1.D[解析]列联表+独立性检验 由题意可知,列联表如下,
| 性别 | 喜爱乒乓球运动 | 不喜爱乒乓球运动 | 合计 |
| --- | --- | --- | --- |
| 男生 | 4m | 2m | 6m |
| 女生 | 3m | 3m | 6m |
| 合计 | 7m | 5m | 12m |
由题意得$\chi^{2}=\frac{12m(4m × 3m - 2m × 3m)^{2}}{6m × 6m × 7m × 5m} = \frac{12m}{35} \geq 7.879$,解得$m \geq 22.98$,因为$m \in \mathbf{N}^{*}$,所以$m$的最小值为$23$。故选D。
| 性别 | 喜爱乒乓球运动 | 不喜爱乒乓球运动 | 合计 |
| --- | --- | --- | --- |
| 男生 | 4m | 2m | 6m |
| 女生 | 3m | 3m | 6m |
| 合计 | 7m | 5m | 12m |
由题意得$\chi^{2}=\frac{12m(4m × 3m - 2m × 3m)^{2}}{6m × 6m × 7m × 5m} = \frac{12m}{35} \geq 7.879$,解得$m \geq 22.98$,因为$m \in \mathbf{N}^{*}$,所以$m$的最小值为$23$。故选D。
2. 为了验证牛的毛色(黑色、红色)和角(有角、无角)这两对相对性状是否相关,某学院进行了一次数据统计,并根据形成的 $2× 2$ 列联表,计算得到 $\chi ^{2}\approx 2.727$ ,根据小概率值为 $\alpha$ 的独立性检验,则 (
附:

A.若 $\alpha =0.100$ ,则认为“毛色”和“角”无关
B.若 $\alpha =0.100$ ,则认为“毛色”和“角”有关,此推断犯错误的概率不超过 $10\%$
C.若 $\alpha =0.010$ ,则认为“毛色”和“角”无关
D.若 $\alpha =0.010$ ,则认为“毛色”和“角”有关,此推断犯错误的概率不超过 $1\%$
BC
)附:

A.若 $\alpha =0.100$ ,则认为“毛色”和“角”无关
B.若 $\alpha =0.100$ ,则认为“毛色”和“角”有关,此推断犯错误的概率不超过 $10\%$
C.若 $\alpha =0.010$ ,则认为“毛色”和“角”无关
D.若 $\alpha =0.010$ ,则认为“毛色”和“角”有关,此推断犯错误的概率不超过 $1\%$
答案:
2.BC[解析]独立性检验 对于A,B,若$\alpha = 0.100$,因为$2.706 < 2.727$,则认为“毛色”和“角”有关,此推断犯错误的概率不超过$10\%$,故A错误,B正确。对于C,D,若$\alpha = 0.010$,因为$6.635 > 2.727$,则认为“毛色”和“角”无关,故C正确,D错误。故选BC。
方法技巧
基于小概率值$\alpha$的检验规则:当$\chi^{2} \geq x_{\alpha}$时,我们就推断$H_{0}$不成立,即认为$X$和$Y$不独立,该推断犯错误的概率不超过$\alpha$;当$\chi^{2} < x_{\alpha}$时,我们没有充分证据推断$H_{0}$不成立,可以认为$X$和$Y$独立。
方法技巧
基于小概率值$\alpha$的检验规则:当$\chi^{2} \geq x_{\alpha}$时,我们就推断$H_{0}$不成立,即认为$X$和$Y$不独立,该推断犯错误的概率不超过$\alpha$;当$\chi^{2} < x_{\alpha}$时,我们没有充分证据推断$H_{0}$不成立,可以认为$X$和$Y$独立。
3. 下列结论正确的是 (
A.当研究两个变量之间的关联程度时,若相关系数的绝对值 $|r|$ 越接近于 $1$ ,则两个变量的线性相关程度越弱
B.在评估模型拟合效果时,决定系数 $R^{2}$ 越接近于 $1$ ,表示模型对数据的拟合效果越好
C.通过样本数据得到的回归直线 $\hat {y}=\hat {b}x+\hat {a}$ 一定经过点 $(\overline {x},\overline {y})$
D.设关于分类变量 $X$ 与 $Y$ 的独立性检验的原假设为 $H_{0}:X$ 与 $Y$ 无关,根据分类变量 $X$ 与 $Y$ 的成对样本数据,计算得到 $\chi ^{2}=4.172$ ,依据 $\alpha =0.05$ 的独立性检验 $(\chi _{0.05}=3.841)$ ,没有充分证据推断 $H_{0}$ 不成立,即认为 $X$ 与 $Y$ 无关
BC
)A.当研究两个变量之间的关联程度时,若相关系数的绝对值 $|r|$ 越接近于 $1$ ,则两个变量的线性相关程度越弱
B.在评估模型拟合效果时,决定系数 $R^{2}$ 越接近于 $1$ ,表示模型对数据的拟合效果越好
C.通过样本数据得到的回归直线 $\hat {y}=\hat {b}x+\hat {a}$ 一定经过点 $(\overline {x},\overline {y})$
D.设关于分类变量 $X$ 与 $Y$ 的独立性检验的原假设为 $H_{0}:X$ 与 $Y$ 无关,根据分类变量 $X$ 与 $Y$ 的成对样本数据,计算得到 $\chi ^{2}=4.172$ ,依据 $\alpha =0.05$ 的独立性检验 $(\chi _{0.05}=3.841)$ ,没有充分证据推断 $H_{0}$ 不成立,即认为 $X$ 与 $Y$ 无关
答案:
3.BC[解析]回归直线方程+独立性检验 相关系数的绝对值$|r|$越接近于$1$,两个变量的线性相关程度越强,故A错误。决定系数$R^{2}$越接近于$1$,表示模型对数据的拟合效果越好,故B正确。因为回归直线$\hat{y} = \hat{b}x + \hat{a}$一定经过样本点的中心,即$(\bar{x},\bar{y})$,故C正确。因为$\chi^{2} = 4.172>3.841$,所以应拒绝原假设$H_{0}$,即认为$X$与$Y$有关。故D错误。故选BC。
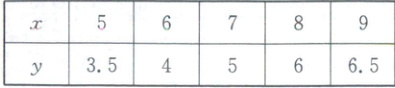
4. 已知变量 $x,y$ 的统计数据如表,对表中数据作分析,发现 $y$ 与 $x$ 之间具有线性相关关系,利用最小二乘法,计算得到回归直线方程为 $\hat {y}=0.8x+\hat {a}$ ,据此模型预测当 $x=10$ 时, $\hat {y}$ 的值为
7.4
.
答案:
4.7.4 [解析]回归直线方程 由表格数据,得$\bar{x} = \frac{5 + 6 + 7 + 8 + 9}{5} = 7$,$\bar{y} = \frac{3.5 + 4 + 5 + 6 + 6.5}{5} = 5$。因为回归直线$\hat{y} = 0.8x + \hat{a}$过样本点的中心$(7,5)$,所以$5 = 0.8 × 7 + \hat{a}$,解得$\hat{a} = - 0.6$。所以$\hat{y} = 0.8x - 0.6$,当$x = 10$时,$\hat{y} = 0.8 × 10 - 0.6 = 7.4$。
查看更多完整答案,请扫码查看


