《2025年天利38套对接高考单元专题测试卷高中数学选择性必修第二册人教版》

18. (17 分)为了测试一种新药对某种疾病的治疗效果，研究人员对一地区某种动物种群（数量较大）进行试验，从该试验种群中随机抽查了 80 只，得到如下的样本数据（单位：只）：


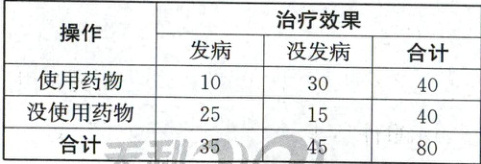
(1) 能否在犯错误的概率不超过 0.001 的前提下，认为该药物与预防该疾病有关？
(2) 从该地区此动物群中任取一只，记$A$表示此动物发病，$\overline{A}$表示此动物没发病，$B$表示此动物使用药物，定义事件$A$的优势$R_{1}=\frac{P(A)}{1 - P(A)}$. 在事件$B$发生的条件下$A$的优势$R_{2}=\frac{P(A|B)}{1 - P(A|B)}$. 证明：$\frac{R_{2}}{R_{1}}=\frac{P(B|A)}{P(B|\overline{A})}$，并利用表中数据求出$\frac{R_{2}}{R_{1}}$的值.
(3) 若把表中的频率视作概率，现从该地区没发病的动物中抽取 3 只动物，记抽取的 3 只动物中使用药物的只数为$X$，求随机变量$X$的分布列、数学期望.
附：$\chi^{2}=\frac{n(ad - bc)^{2}}{(a + b)(c + d)(a + c)(b + d)}$，其中$n = a + b + c + d$.

答案： 18.独立性检验+条件概率+对立事件的概率公式+全概
率公式+二项分布+离散型随机变量的分布列与数学
期望
解：
(1)提出假设 $H_0$：使用该药物与预防该疾病无关，
根据题中列联表可得 $\chi^2=\frac {80×(10×15-30×25)^2}{40×40×35×45}\approx$
11.429＞10.828，
所以在犯错误的概率不超过0.001的前提下，推断
$H_0$ 不成立，即认为使用该药物与预防该疾病有关(提
示：零假设为否定假设，计算的 $\chi^2$ 值如果大于相应的
小概率值，假设不成立，如果小于相应的小概率值，则
假设成立).
(4分)
(2)证明：由于 $1-P(A|B)=1-\frac {P(AB)}{P(B)}=$
$\frac {P(B)-P(AB)}{P(B)}=\frac {P(\overline{A}B)}{P(B)}=P(\overline{A}|B)$,
所以 $R_2=\frac {P(A|B)}{1-P(A|B)}=\frac {P(A|B)}{P(\overline{A}|B)}$
因为 $R_1=\frac {P(A)}{1-P(A)}=\frac {P(A)}{P(\overline{A})}$，
则 $\frac {R_2}{R_1}=\frac {P(A|B)}{P(\overline{A}|B)}×\frac {P(\overline{A})}{P(A)}=\frac {P(A|B)P(\overline{A})}{P(\overline{A}|B)P(A)}=$
$\frac {P(AB)}{P(A)}×\frac {P(\overline{A})}{P(\overline{A}|B)P(A)}=\frac {P(AB)}{P(A)}×\frac {P(\overline{A})}{P(\overline{A}|B)P(A)}$(提示：利用条件概率的概率公式、
$P(AB)P(A)$
$P(A)$ 对立事件的概率公式以及全概率公式进行化简).
由题中列联表中的数据可得 $P(B|A)=\frac {10}{35}=\frac {2}{7}$,
$P(B|\overline{A})=\frac {30}{45}=\frac {2}{3}$，
所以 $\frac {R_2}{R_1}=\frac {3}{7}$.
(10分)
(3)由题可知，抽查的45只没发病的动物中使用该药
物和没使用该药物的动物分别为30只和15只，所以从没
发病的动物中随机抽取1只，抽取的是使用了该
药物的概率为 $\frac {30}{45}=\frac {2}{3}$，
则由题意可知 $X=0,1,2,3$，且 $X\sim B(3,\frac {2}{3})$(题眼)
(12分)
则 $P(X=0)=\mathrm{C}_3^0(\frac {1}{3})^3=\frac {1}{27}$,
$P(X=1)=\mathrm{C}_3^1(\frac {2}{3})^1(\frac {1}{3})^2=\frac {6}{27}=\frac {2}{9}$,
$P(X=2)=\mathrm{C}_3^2(\frac {2}{3})^2(\frac {1}{3})^1=\frac {12}{27}=\frac {4}{9}$,
$P(X=3)=\mathrm{C}_3^3(\frac {2}{3})^3=\frac {8}{27}$,
(15分)
所以随机变量 $X$ 的分布列为：
$X$ 0 1 2 3
$P$ $\frac {1}{27}$ $\frac {2}{9}$ $\frac {4}{9}$ $\frac {8}{27}$
随机变量 $X$ 的数学期望 $E(X)=3×\frac {2}{3}=2$.
(17分)
知识延伸
二项分布的数学期望和方差公式 若 $X\sim B(n,p)$，
则 $E(X)=np$,$D(X)=np(1-p)$.