《2025年天利38套对接高考单元专题测试卷高中数学选择性必修第二册人教版》

12. 若$(1 - ax)^6(a\neq0)$展开式的各二项式系数的和是其系数和的64倍，则实数$a$的值为_。2

答案： 12.2【解析】二项式定理$(1-ax)^6(a\neq0)$展开式中各二项式系数的和为$2^6$，系数和为$(1-a)^6$.$\because2^6=64(1-a)^6=(2-2a)^6$，$\therefore2=\pm(2-2a)$.又$a\neq0$.故$2=2a-2$，解得$a=2$.

13. 为深入学习贯彻党的二十大精神，推动全市党员干部群众用好“学习强国”学习平台，某单位组织“学习强国”知识竞赛，竞赛共有10道题目，随机抽取3道让参赛者回答，规定参赛者至少要答对其中2道才能通过初试。已知某参赛党员甲只能答对其中的6道，那么党员甲抽到能答对题目数$X$的数学期望为_；党员甲能通过初试的概率为_。$\frac{9}{5}$ $\frac{2}{3}$

答案： 13.$\frac{9}{5}\frac{2}{3}$【解析】超几何分布+离散型随机变量的数学期望由题意可知，X的所有可能取值为0,1,2,3，则$P(X=0)=\frac{C_4^3}{C_{10}^3}=\frac{1}{30}$，$P(X=1)=\frac{C_4^2C_4^1}{C_{10}^3}=\frac{3}{10}$，$P(X=2)=\frac{C_4^1C_4^2}{C_{10}^3}=\frac{1}{2}$，$P(X=3)=\frac{C_4^0C_4^3}{C_{10}^3}=\frac{1}{6}$，$\therefore E(X)=0×\frac{1}{30}+1×\frac{3}{10}+2×\frac{1}{2}+3×\frac{1}{6}=\frac{9}{5}$.党员甲能通过初试的概率为$P(X=2)+P(X=3)=\frac{1}{2}+\frac{1}{6}=\frac{2}{3}$.

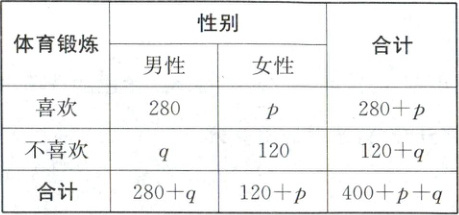
14. 为了提高学生体育锻炼的积极性，某中学需要了解性别因素与学生对体育锻炼的喜好是否有影响，为此对学生是否喜欢体育锻炼的情况进行普查，得到下表：

附：$\chi^2=\frac{n(ad - bc)^2}{(a + b)(c + d)(a + c)(b + d)}$，其中$n = a + b + c + d$。

已知男生喜欢体育锻炼的人数占男生人数的$\frac{7}{10}$，女生喜欢体育锻炼的人数占女生人数的$\frac{3}{5}$，则下列说法正确的是_。①③④
①列表中$q$的值为120，$p$的值为180
②随机对一名学生进行调查，此学生有90%的可能性喜欢体育锻炼
③根据小概率值$\alpha = 0.01$的独立性检验，男、女生对体育锻炼的喜好有差异
④根据小概率值$\alpha = 0.001$的独立性检验，男、女生对体育锻炼的喜好没有差异

答案： 14.①③④【解析】独立性检验对于①，男生喜欢体育锻炼的人数占男生人数的$\frac{7}{10}$，女生喜欢体育锻炼的人数占女生人数的$\frac{3}{5}$，所以$280=\frac{7}{10}(280+q)$，且$p=\frac{3}{5}(120+p)$，解得$q=120$，$p=180$.故①正确.对于②，补全$2×2$列联表（题眼），所以随机对一名学生进行调查，喜欢体育锻炼的概率为$\frac{460}{700}\approx65.7\%$.故②错误.对于③，$\chi^2=\frac{n(ad-bc)^2}{(a+b)(c+d)(a+c)(b+d)}=\frac{700(280×120-180×120)^2}{460×240×400×300}\approx7.609$（题眼），而$6.635＜7.609＜10.828$，所以根据小概率值$\alpha=0.01$的独立性检验，可知男、女生对体育锻炼的喜好有差异.故③正确.对于④，根据小概率值$\alpha=0.001$的独立性检验（题眼），可知男、女生对体育锻炼的喜好没有差异.故④正确.故选①③④.

15. （13分）某车企为考察选购新能源汽车的款式与性别的关联性，调查100人购买情况，得到如下列联表：

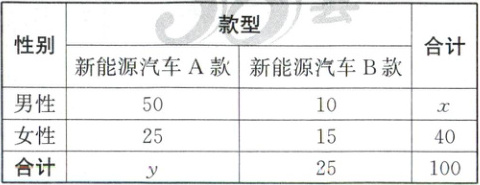
（1）求$x$，$y$。
（2）根据小概率值$\alpha = 0.05$的独立性检验，能否认为选购该新能源汽车的款式与性别有关联？
（3）假设用样本估计总体，用频率估计概率，所有人选购汽车的款式情况相互独立。若从购买者中随机抽取3人，设被抽取的3人中购买了B款车的人数为$X$，求$X$的数学期望。
附：$\chi^2=\frac{n(ad - bc)^2}{(a + b)(c + d)(a + c)(b + d)}$，其中$n = a + b + c + d$。

答案： 15.独立性检验+二项分布
解：
(1)$x=60$，$y=75$（提示：由题表得$x=50+10=60$，$y=100-25=75$）.
(2)零假设为$H_0$：选购新能源汽车的款式与性别无关联.
根据题中列联表中的数据，可得$\chi^2=\frac{100×(50×15-25×10)^2}{75×25×60×40}\approx5.556＞3.841$，根据小概率值$\alpha=0.05$的独立性检验，推断$H_0$不成立，能认为选购新能源汽车的款式与性别有关联，此推断犯错误的概率不大于0.05（提醒：对判断结果进行描述时，注意对象的选取要准确无误，应是对假设结论进行的含概率的判断，而非其他，要避免张冠李戴）.
(3)随机抽取1人购买B款车的概率为$p=\frac{25}{100}=\frac{1}{4}$，依题意$X$服从二项分布$B(3,\frac{1}{4})$（题眼）（提醒：在求随机变量的期望时，首先判断随机变量是否服从两点分布、二项分布或超几何分布.若服从，则可直接用公式求期望）.
因此，$E(X)=3×\frac{1}{4}=\frac{3}{4}$.（13分）