2025年天利38套对接高考单元专题测试卷高中数学选择性必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年天利38套对接高考单元专题测试卷高中数学选择性必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
17. (15 分)(2024·上海卷)为了了解某地初中学生体育日均锻炼时长与学业成绩的关系,从该地区 29 000 名学生中抽取 580 人,得到日均体育锻炼时长(单位:h)与学业成绩的数据如表所示:

(1) 该地区 29 000 名学生中日均体育锻炼时长不少于 1 h 的人数约为多少?
(2) 估计该地区初中学生日均体育锻炼的时长(精确到 0.1)。
(3) 是否有 $ 95\% $ 的把握认为“学业成绩优秀”与“日均体育锻炼时长不小于 1 h 且小于 2 h”有关?
附:$ \chi^2 = \frac{n(ad - bc)^2}{(a + b)(c + d)(a + c)(b + d)} $,其中 $ n = a + b + c + d $。$ P(\chi^2 \geq 3.841) \approx 0.05 $。

(1) 该地区 29 000 名学生中日均体育锻炼时长不少于 1 h 的人数约为多少?
(2) 估计该地区初中学生日均体育锻炼的时长(精确到 0.1)。
(3) 是否有 $ 95\% $ 的把握认为“学业成绩优秀”与“日均体育锻炼时长不小于 1 h 且小于 2 h”有关?
附:$ \chi^2 = \frac{n(ad - bc)^2}{(a + b)(c + d)(a + c)(b + d)} $,其中 $ n = a + b + c + d $。$ P(\chi^2 \geq 3.841) \approx 0.05 $。
答案:
17.用样本估计总体+平均数+独立性检验
【思维导图】
(1)确定580人中日均体育锻炼时长不少于1小时的比例$\rightarrow$该地区29000名学生中日均体育锻炼时长不少于1小时的人数。
(2)由时间范围计算每组中值$\rightarrow$平均数。
(3)已知条件$\rightarrow$提出原假设$H_{0} \rightarrow$求出$\chi^{2} \rightarrow$比较大小$\rightarrow$得解。
解:
(1)$\because$抽取的580人中日均体育锻炼时长不少于1h的人数占比为$\frac{42 + 3 + 1 + 137 + 40 + 27}{580}=\frac{25}{58}$,
$\therefore$该地区29000名学生中日均体育锻炼时长不少于1h的人数约为$29000 × \frac{25}{58}=12500$(人)。
(2)该地区初中学生日均体育锻炼的时长约为$\frac{1}{580} × [\frac{0.5}{2} × (5 + 134) + \frac{0.5 + 1}{2} × (44 + 147) + \frac{1 + 1.5}{2} × (42 + 137) + \frac{1.5 + 2}{2} × (3 + 40) + \frac{2 + 2.5}{2} × (1 + 27)]=\frac{27}{29} \approx 0.9$。
(3)作出列联表如下:
|日均体育锻炼时长|$[1,2)$|其他|合计|
|----|----|----|----|
|学业成绩优秀人数|45|50|95|
|学业成绩不优秀人数|177|308|485|
|合计|222|358|580|
提出原假设$H_{0}$:“学业成绩优秀”与“日均体育锻炼时长不小于1h且小于2h”无关。
$\chi^{2}=\frac{580 × (45 × 308 - 50 × 177)^{2}}{95 × 485 × 222 × 358} \approx 3.976 > 3.841$,
即根据小概率值$\alpha = 0.05$的独立性检验,我们推断$H_{0}$不成立,
即“学业成绩优秀”与“日均体育锻炼时长不小于1h且小于2h”有关,
$\therefore$有95%的把握认为“学业成绩优秀”与“日均体育锻炼时长不小于1h且小于2h”有关。
【思维导图】
(1)确定580人中日均体育锻炼时长不少于1小时的比例$\rightarrow$该地区29000名学生中日均体育锻炼时长不少于1小时的人数。
(2)由时间范围计算每组中值$\rightarrow$平均数。
(3)已知条件$\rightarrow$提出原假设$H_{0} \rightarrow$求出$\chi^{2} \rightarrow$比较大小$\rightarrow$得解。
解:
(1)$\because$抽取的580人中日均体育锻炼时长不少于1h的人数占比为$\frac{42 + 3 + 1 + 137 + 40 + 27}{580}=\frac{25}{58}$,
$\therefore$该地区29000名学生中日均体育锻炼时长不少于1h的人数约为$29000 × \frac{25}{58}=12500$(人)。
(2)该地区初中学生日均体育锻炼的时长约为$\frac{1}{580} × [\frac{0.5}{2} × (5 + 134) + \frac{0.5 + 1}{2} × (44 + 147) + \frac{1 + 1.5}{2} × (42 + 137) + \frac{1.5 + 2}{2} × (3 + 40) + \frac{2 + 2.5}{2} × (1 + 27)]=\frac{27}{29} \approx 0.9$。
(3)作出列联表如下:
|日均体育锻炼时长|$[1,2)$|其他|合计|
|----|----|----|----|
|学业成绩优秀人数|45|50|95|
|学业成绩不优秀人数|177|308|485|
|合计|222|358|580|
提出原假设$H_{0}$:“学业成绩优秀”与“日均体育锻炼时长不小于1h且小于2h”无关。
$\chi^{2}=\frac{580 × (45 × 308 - 50 × 177)^{2}}{95 × 485 × 222 × 358} \approx 3.976 > 3.841$,
即根据小概率值$\alpha = 0.05$的独立性检验,我们推断$H_{0}$不成立,
即“学业成绩优秀”与“日均体育锻炼时长不小于1h且小于2h”有关,
$\therefore$有95%的把握认为“学业成绩优秀”与“日均体育锻炼时长不小于1h且小于2h”有关。
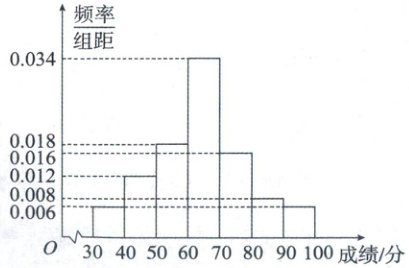
18. (17 分)某市为了传承发展中华优秀传统文化,组织该市中学生进行了一次文化知识有奖竞赛,竞赛奖励规则如下:得分在 $[70,80)$ 内的学生获三等奖,得分在 $[80,90)$ 内的学生获二等奖,得分在 $[90,100]$ 内的学生获一等奖,其他学生不得奖;为了了解学生对相关知识的掌握情况,随机抽取 100 名学生的竞赛成绩,并以此为样本绘制了样本频率分布直方图,如图所示。若该市所有参赛学生的成绩 $ X $ 近似服从正态分布 $ N(\mu,\sigma^2) $,其中 $ \sigma \approx 15 $,$ \mu $ 为样本平均数的估计值,利用所得正态分布模型解决以下问题:
(1) 若该市共有 10 000 名学生参加了竞赛,试估计参赛学生中成绩超过 79 分的学生数(结果四舍五入到整数)。
(2) 若从所有参赛学生中(参赛学生数大于 10 000)随机抽取 3 名学生进行访谈,设其中竞赛成绩在 64 分以上的学生数为 $ \xi $,求随机变量 $ \xi $ 的分布列和均值。
附:若随机变量 $ X $ 服从正态分布 $ N(\mu,\sigma^2) $,则 $ P(\mu - \sigma < X \leq \mu + \sigma) \approx 0.6826 $,$ P(\mu - 2\sigma < X \leq \mu + 2\sigma) \approx 0.9544 $,$ P(\mu - 3\sigma < X \leq \mu + 3\sigma) \approx 0.9974 $。

(1) 若该市共有 10 000 名学生参加了竞赛,试估计参赛学生中成绩超过 79 分的学生数(结果四舍五入到整数)。
(2) 若从所有参赛学生中(参赛学生数大于 10 000)随机抽取 3 名学生进行访谈,设其中竞赛成绩在 64 分以上的学生数为 $ \xi $,求随机变量 $ \xi $ 的分布列和均值。
附:若随机变量 $ X $ 服从正态分布 $ N(\mu,\sigma^2) $,则 $ P(\mu - \sigma < X \leq \mu + \sigma) \approx 0.6826 $,$ P(\mu - 2\sigma < X \leq \mu + 2\sigma) \approx 0.9544 $,$ P(\mu - 3\sigma < X \leq \mu + 3\sigma) \approx 0.9974 $。
答案:
18.正态分布+随机变量的分布列与均值
解:
(1)由频率分布直方图知,各小矩形面积从左到右依次为0.06,0.12,0.18,0.34,0.16,0.08,0.06,
样本平均数的估计值$\mu = 0.06 × 35 + 0.12 × 45 + 0.18 × 55 + 0.34 × 65 + 0.16 × 75 + 0.08 × 85 + 0.06 × 95 = 64$,
则所有参赛学生的成绩X近似服从正态分布$N(64,15^{2})$,而$\mu + \sigma = 79$,
因此$P(X > 79)=P(X > \mu + \sigma) \approx \frac{1 - 0.6826}{2}=0.1587$。
所以参赛学生中成绩超过79分的学生数约为$0.1587 × 10000 = 1587$。
(2)由
(1)知,$\mu = 64$,$P(X > 64)=\frac{1}{2}$,
即从所有参赛学生中随机抽取1名学生,该学生竞赛成绩在64分以上的概率为$\frac{1}{2}$,
因此随机变量$\xi$服从二项分布$\xi \sim B(3,\frac{1}{2})$,$\xi$的所有可能取值为0,1,2,3,
则$P(\xi = 0)=C_{3}^{0}(\frac{1}{2})^{3}=\frac{1}{8}$,
$P(\xi = 1)=C_{3}^{1}(\frac{1}{2})^{3}=\frac{3}{8}$,
$P(\xi = 2)=C_{3}^{2}(\frac{1}{2})^{3}=\frac{3}{8}$,
$P(\xi = 3)=C_{3}^{3}(\frac{1}{2})^{3}=\frac{1}{8}$,
所以随机变量$\xi$的分布列为
|$\xi$|0|1|2|3|
|----|----|----|----|----|
|$P$|$\frac{1}{8}$|$\frac{3}{8}$|$\frac{3}{8}$|$\frac{1}{8}$|
故数学期望$E(\xi)=0 × \frac{1}{8} + 1 × \frac{3}{8} + 2 × \frac{3}{8} + 3 × \frac{1}{8}=\frac{3}{2}$。
解:
(1)由频率分布直方图知,各小矩形面积从左到右依次为0.06,0.12,0.18,0.34,0.16,0.08,0.06,
样本平均数的估计值$\mu = 0.06 × 35 + 0.12 × 45 + 0.18 × 55 + 0.34 × 65 + 0.16 × 75 + 0.08 × 85 + 0.06 × 95 = 64$,
则所有参赛学生的成绩X近似服从正态分布$N(64,15^{2})$,而$\mu + \sigma = 79$,
因此$P(X > 79)=P(X > \mu + \sigma) \approx \frac{1 - 0.6826}{2}=0.1587$。
所以参赛学生中成绩超过79分的学生数约为$0.1587 × 10000 = 1587$。
(2)由
(1)知,$\mu = 64$,$P(X > 64)=\frac{1}{2}$,
即从所有参赛学生中随机抽取1名学生,该学生竞赛成绩在64分以上的概率为$\frac{1}{2}$,
因此随机变量$\xi$服从二项分布$\xi \sim B(3,\frac{1}{2})$,$\xi$的所有可能取值为0,1,2,3,
则$P(\xi = 0)=C_{3}^{0}(\frac{1}{2})^{3}=\frac{1}{8}$,
$P(\xi = 1)=C_{3}^{1}(\frac{1}{2})^{3}=\frac{3}{8}$,
$P(\xi = 2)=C_{3}^{2}(\frac{1}{2})^{3}=\frac{3}{8}$,
$P(\xi = 3)=C_{3}^{3}(\frac{1}{2})^{3}=\frac{1}{8}$,
所以随机变量$\xi$的分布列为
|$\xi$|0|1|2|3|
|----|----|----|----|----|
|$P$|$\frac{1}{8}$|$\frac{3}{8}$|$\frac{3}{8}$|$\frac{1}{8}$|
故数学期望$E(\xi)=0 × \frac{1}{8} + 1 × \frac{3}{8} + 2 × \frac{3}{8} + 3 × \frac{1}{8}=\frac{3}{2}$。
查看更多完整答案,请扫码查看


