2025年通城学典非常课课通九年级数学上册人教版江苏专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年通城学典非常课课通九年级数学上册人教版江苏专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
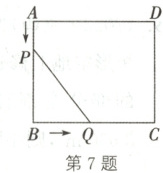
7. 如图,在矩形ABCD中,AB = 5cm,BC = 6cm,点P从点A开始沿边AB向终点B以1cm/s的速度运动,点Q从点B开始沿边BC向终点C以2cm/s的速度运动。点P,Q分别从点A,B同时出发,当点Q运动到点C时,两点停止运动。设运动时间为t(t > 0)s。
(1)当t为何值时,PQ的长为5cm?
(2)是否存在t的值,使得五边形APQCD的面积为26cm²?若存在,请求出此时t的值;若不存在,请说明理由。
(1)当t为何值时,PQ的长为5cm?
(2)是否存在t的值,使得五边形APQCD的面积为26cm²?若存在,请求出此时t的值;若不存在,请说明理由。

答案:
7.
(1)由题意,得$AP = t cm$,$BP = (5 - t)cm$,$BQ = 2t cm$,$PQ = 5cm$。在$Rt\triangle BPQ$中,$BP^{2} + BQ^{2} = PQ^{2}$,
$\therefore(5 - t)^{2} + (2t)^{2} = 5^{2}$,解得$t_{1} = 0$(不合题意,舍去),
$t_{2} = 2$。$\therefore$当$t = 2$时,$PQ$的长为$5cm$
(2)存在
$\because S_{矩形ABCD} = 5 × 6 = 30(cm^{2})$,$S_{五边形APQCD} = 26cm^{2}$,
$\therefore S_{\triangle PBQ} = 30 - 26 = 4(cm^{2})$。$\therefore$易得$\frac{1}{2} × (5 - t) × 2t = 4$,解得$t_{1} = 4$,$t_{2} = 1$。$\because 6 ÷ 2 = 3(s)$,$\therefore 0 < t \leq 3$。$\therefore$当$t = 1$时,五边形$APQCD$的面积为$26cm^{2}$
(1)由题意,得$AP = t cm$,$BP = (5 - t)cm$,$BQ = 2t cm$,$PQ = 5cm$。在$Rt\triangle BPQ$中,$BP^{2} + BQ^{2} = PQ^{2}$,
$\therefore(5 - t)^{2} + (2t)^{2} = 5^{2}$,解得$t_{1} = 0$(不合题意,舍去),
$t_{2} = 2$。$\therefore$当$t = 2$时,$PQ$的长为$5cm$
(2)存在
$\because S_{矩形ABCD} = 5 × 6 = 30(cm^{2})$,$S_{五边形APQCD} = 26cm^{2}$,
$\therefore S_{\triangle PBQ} = 30 - 26 = 4(cm^{2})$。$\therefore$易得$\frac{1}{2} × (5 - t) × 2t = 4$,解得$t_{1} = 4$,$t_{2} = 1$。$\because 6 ÷ 2 = 3(s)$,$\therefore 0 < t \leq 3$。$\therefore$当$t = 1$时,五边形$APQCD$的面积为$26cm^{2}$
8. 某商场于今年年初以25元/件的进价购进一批商品。当商品的售价为40元/件时,1月销售了256件。2,3月该商品十分畅销,销售量持续走高。在售价不变的基础上,3月的销售量达到了400件。
(1)求2,3月销售量的月平均增长率。
(2)从4月起,商场决定采用降价促销的方式回馈顾客,经调查发现,该商品每件每降价2元,销售量增加10件。当每件商品降价多少元时,商场当月获利4250元?
(1)求2,3月销售量的月平均增长率。
(2)从4月起,商场决定采用降价促销的方式回馈顾客,经调查发现,该商品每件每降价2元,销售量增加10件。当每件商品降价多少元时,商场当月获利4250元?
答案:
8.
(1)设2,3月销售量的月平均增长率为$x$。根据题意,
得$256(1 + x)^{2} = 400$,解得$x_{1} = 0.25 = 25\%$,$x_{2} = - 2.25$(不合题意,舍去)。$\therefore$2,3月销售量的月平均增长率为$25\%$
(2)设每件商品降价$y$元。根据题意,得$(40 - y - 25)(400 + \frac{10}{2}y) = 4250$。整理,得$y^{2} + 65y - 350 = 0$,解得$y_{1} = 5$,$y_{2} = - 70$(不合题意,舍去)。$\therefore$当每件商品降价$5$元时,商场当月获利$4250$元
(1)设2,3月销售量的月平均增长率为$x$。根据题意,
得$256(1 + x)^{2} = 400$,解得$x_{1} = 0.25 = 25\%$,$x_{2} = - 2.25$(不合题意,舍去)。$\therefore$2,3月销售量的月平均增长率为$25\%$
(2)设每件商品降价$y$元。根据题意,得$(40 - y - 25)(400 + \frac{10}{2}y) = 4250$。整理,得$y^{2} + 65y - 350 = 0$,解得$y_{1} = 5$,$y_{2} = - 70$(不合题意,舍去)。$\therefore$当每件商品降价$5$元时,商场当月获利$4250$元
9. 如图所示为一张月历,在此月历上可以用一个矩形任意圈出2×2个位置相邻的数(如2,3,9,10)。若圈出的4个数中最大数与最小数的积为128,则这4个数中最小的数是
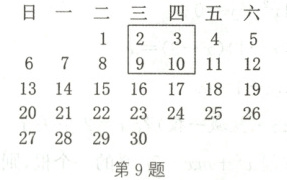
8
。
答案:
9. 8
10. 某网店专门销售某种品牌的工艺品,成本为30元/件,每天的销售量y(件)与销售单价x(元)之间存在如图所示的一次函数关系。
(1)求y与x之间的函数解析式。
(2)在确保盈利的情况下,若规定每天工艺品的销售量不低于240件,则销售单价应定在什么范围?
(3)若在(2)的条件下,网店每天销售的利润为3750元,则该种工艺品的销售单价是多少元?

(1)求y与x之间的函数解析式。
(2)在确保盈利的情况下,若规定每天工艺品的销售量不低于240件,则销售单价应定在什么范围?
(3)若在(2)的条件下,网店每天销售的利润为3750元,则该种工艺品的销售单价是多少元?

答案:
10.
(1)设$y$与$x$之间的函数解析式为$y = kx + b(k \neq 0)$。
将$(40,300)$,$(55,150)$代入,得$\begin{cases}40k + b = 300,\\55k + b = 150.\end{cases}$解得$\begin{cases}k = - 10,\\b = 700.\end{cases}$
$\therefore y$与$x$之间的函数解析式为$y = - 10x + 700$
(2)当$y \geq 240$时,$- 10x + 700 \geq 240$,解得$x \leq 46$。
$\because$成本为$30$元/件,$\therefore 30 < x \leq 46$。$\therefore$销售单价应大于$30$元,小于等于$46$元
(3)依题意,得$(x - 30)( - 10x + 700) = 3750$。整理,得$x^{2} - 100x + 2475 = 0$,解得$x_{1} = 45$,$x_{2} = 55$。$\because 30 < x \leq 46$,$\therefore x = 45$。$\therefore$该种工艺品的销售单价是$45$元
(1)设$y$与$x$之间的函数解析式为$y = kx + b(k \neq 0)$。
将$(40,300)$,$(55,150)$代入,得$\begin{cases}40k + b = 300,\\55k + b = 150.\end{cases}$解得$\begin{cases}k = - 10,\\b = 700.\end{cases}$
$\therefore y$与$x$之间的函数解析式为$y = - 10x + 700$
(2)当$y \geq 240$时,$- 10x + 700 \geq 240$,解得$x \leq 46$。
$\because$成本为$30$元/件,$\therefore 30 < x \leq 46$。$\therefore$销售单价应大于$30$元,小于等于$46$元
(3)依题意,得$(x - 30)( - 10x + 700) = 3750$。整理,得$x^{2} - 100x + 2475 = 0$,解得$x_{1} = 45$,$x_{2} = 55$。$\because 30 < x \leq 46$,$\therefore x = 45$。$\therefore$该种工艺品的销售单价是$45$元
查看更多完整答案,请扫码查看


