2025年通城学典非常课课通九年级数学上册人教版江苏专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年通城学典非常课课通九年级数学上册人教版江苏专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
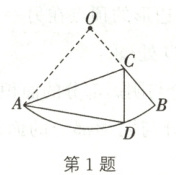
1. 如图,C 为扇形 OAB 的半径 OB 上一点,将△OAC 沿 AC 折叠,点 O 恰好落在$\overset{\frown}{AB}$上的点 D 处,且$l_{\overset{\frown}{BD}}:l_{\overset{\frown}{AD}} = 1:3$。若将此扇形 OAB 围成一个圆锥,则圆锥的底面圆半径与母线长的比为(
A.$1:3$
B.$1:\pi$
C.$1:4$
D.$2:9$
D
)
A.$1:3$
B.$1:\pi$
C.$1:4$
D.$2:9$
答案:
1.D
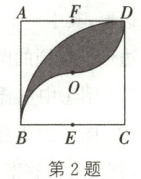
2. (枣庄中考)如图,正方形 ABCD 的边长为 2,O 为对角线的交点,E,F 分别为 BC,AD 的中点。以点 C 为圆心,2 为半径作$\overset{\frown}{BD}$,再分别以点 E,F 为圆心,1 为半径作$\overset{\frown}{BO}$,$\overset{\frown}{OD}$,则图中涂色部分的面积为(
A.$\pi - 1$
B.$\pi - 3$
C.$\pi - 2$
D.$4 - \pi$
C
)
A.$\pi - 1$
B.$\pi - 3$
C.$\pi - 2$
D.$4 - \pi$
答案:
2.C
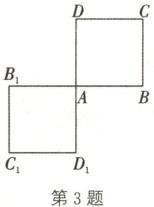
3. 如图,在正方形 ABCD 中,边长$AB = 1$,将正方形 ABCD 绕点 A 按逆时针方向旋转$180^{\circ}$至正方形$AB_{1}C_{1}D_{1}$处,则线段 CD 扫过的面积为(
A.$\frac{\pi}{4}$
B.$\frac{\pi}{2}$
C.$\pi$
D.$2\pi$
B
)
A.$\frac{\pi}{4}$
B.$\frac{\pi}{2}$
C.$\pi$
D.$2\pi$
答案:
3.B
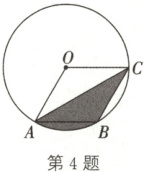
4. 如图,在半径为 6 的$\odot O$中,点 A,B,C 都在$\odot O$上,四边形 OABC 是平行四边形,则图中涂色部分的面积为(
A.$6\pi$
B.$33\pi$
C.$2\sqrt{3}\pi$
D.$2\pi$
A
)
A.$6\pi$
B.$33\pi$
C.$2\sqrt{3}\pi$
D.$2\pi$
答案:
4.A
5. 圆锥侧面展开图的圆心角的度数为$216^{\circ}$,母线长为 5,该圆锥的底面圆半径为
3
。
答案:
5.3
6. 如图,AC 是$\odot O$的直径,B,D 是$\odot O$上的点。若$\odot O$的半径为 3,$\angle ADB = 30^{\circ}$,则$\overset{\frown}{BC}$的长为
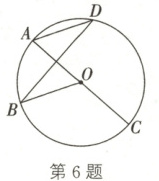
2π
(结果保留$\pi$)。
答案:
6.2π
7. 如图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AC = BC = 2\sqrt{2}$。若把$\triangle ABC$绕边 AB 所在直线旋转一周,则所得几何体的表面积为
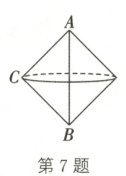
8$\sqrt{2}$π
(结果保留$\pi$)。
答案:
7.8$\sqrt{2}$π
8. 如图,在$Rt\triangle ABC$中,$\angle A = 30^{\circ}$,$AB = 4cm$,将$\triangle ABC$绕顶点 B 按顺时针方向旋转$90^{\circ}$到$\triangle EBD$的位置(结果保留$\pi$)。
(1)点 A 运动的路径长为
(2)点 C 运动的路径长为
(3)线段 BC 扫过的面积为
(4)线段 AB 扫过的面积为
(5)线段 AC 扫过的面积为
(6)$\triangle ABC$扫过的面积为
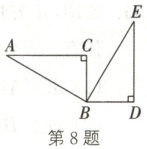
(1)点 A 运动的路径长为
2π cm
;(2)点 C 运动的路径长为
π cm
;(3)线段 BC 扫过的面积为
π cm²
;(4)线段 AB 扫过的面积为
4π cm²
;(5)线段 AC 扫过的面积为
3π cm²
;(6)$\triangle ABC$扫过的面积为
(4π+2$\sqrt{3}$)cm²
。
答案:
8.
(1)2π cm
(2)π cm
(3)π cm²
(4)4π cm²
(5)3π cm²
(6)(4π+2$\sqrt{3}$)cm²
(1)2π cm
(2)π cm
(3)π cm²
(4)4π cm²
(5)3π cm²
(6)(4π+2$\sqrt{3}$)cm²
9. 如图,四边形 ABCD 是正方形,以边 AB 为直径作$\odot O$,点 E 在边 BC 上,连接 AE 交$\odot O$于点 F,连接 BF 并延长,交 CD 于点 G。
(1)求证:$\triangle ABE\cong\triangle BCG$;
(2)若$\angle AEB = 55^{\circ}$,$OA = 3$,求$\overset{\frown}{BF}$的长(结果保留$\pi$)。

(1)求证:$\triangle ABE\cong\triangle BCG$;
(2)若$\angle AEB = 55^{\circ}$,$OA = 3$,求$\overset{\frown}{BF}$的长(结果保留$\pi$)。

答案:
9.
(1)
∵四边形ABCD是正方形,AB是⊙O的直径,
∴AB=BC,∠ABE=∠BCG=∠AFB=90°.
∴∠BAF+∠ABF=90°,∠ABF+∠EBF=90°.
∴∠EBF=∠BAF. 在△ABE和△BCG中,
$\begin{cases} \angle BAE = \angle CBG, \\ \angle ABE = \angle BCG, \\ AB = BC. \end{cases}$
∴△ABE≌△BCG
(2)如图,连接OF.
∵∠ABE=90°,∠AEB=55°,
∴∠BAE=90° - 55°=35°.
∴∠BOF=2∠BAE=70°.
∵OA=3,
∴BF的长为$\frac{70\pi×3}{180}=\frac{7\pi}{6}$

9.
(1)
∵四边形ABCD是正方形,AB是⊙O的直径,
∴AB=BC,∠ABE=∠BCG=∠AFB=90°.
∴∠BAF+∠ABF=90°,∠ABF+∠EBF=90°.
∴∠EBF=∠BAF. 在△ABE和△BCG中,
$\begin{cases} \angle BAE = \angle CBG, \\ \angle ABE = \angle BCG, \\ AB = BC. \end{cases}$
∴△ABE≌△BCG
(2)如图,连接OF.
∵∠ABE=90°,∠AEB=55°,
∴∠BAE=90° - 55°=35°.
∴∠BOF=2∠BAE=70°.
∵OA=3,
∴BF的长为$\frac{70\pi×3}{180}=\frac{7\pi}{6}$

查看更多完整答案,请扫码查看


