2025年通城学典非常课课通九年级数学上册人教版江苏专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年通城学典非常课课通九年级数学上册人教版江苏专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
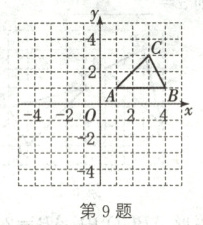
9. 如图,在平面直角坐标系中,$ \triangle ABC $ 三个顶点的坐标分别是 $ A(1,1) $,$ B(4,1) $,$ C(3,3) $。
(1)将 $ \triangle ABC $ 向下平移 $ 5 $ 个单位长度后得到 $ \triangle A_1B_1C_1 $,请画出 $ \triangle A_1B_1C_1 $;
(2)将 $ \triangle ABC $ 绕原点 $ O $ 按逆时针方向旋转 $ 90^{\circ} $ 后得到 $ \triangle A_2B_2C_2 $,请画出 $ \triangle A_2B_2C_2 $;
(3)判断以 $ O $,$ A_1 $,$ B $ 为顶点的三角形的形状。
(1)将 $ \triangle ABC $ 向下平移 $ 5 $ 个单位长度后得到 $ \triangle A_1B_1C_1 $,请画出 $ \triangle A_1B_1C_1 $;
(2)将 $ \triangle ABC $ 绕原点 $ O $ 按逆时针方向旋转 $ 90^{\circ} $ 后得到 $ \triangle A_2B_2C_2 $,请画出 $ \triangle A_2B_2C_2 $;
(3)判断以 $ O $,$ A_1 $,$ B $ 为顶点的三角形的形状。

答案:
9.
(1)如图,$\triangle A_{1}B_{1}C_{1}$即为所求作
(2)如图,$\triangle A_{2}B_{2}C_{2}$即为所求作
(3)如图,连接$OA_{1}$,$OB$,$A_{1}B$.
∵$OB = OA_{1} = \sqrt{4^{2}+1^{2}} = \sqrt{17}$,$A_{1}B = \sqrt{5^{2}+3^{2}} = \sqrt{34}$,即$OB^{2}+OA_{1}^{2} = A_{1}B^{2}$,
∴以$O$,$A_{1}$,$B$为顶点的三角形的形状为等腰直角三角形

9.
(1)如图,$\triangle A_{1}B_{1}C_{1}$即为所求作
(2)如图,$\triangle A_{2}B_{2}C_{2}$即为所求作
(3)如图,连接$OA_{1}$,$OB$,$A_{1}B$.
∵$OB = OA_{1} = \sqrt{4^{2}+1^{2}} = \sqrt{17}$,$A_{1}B = \sqrt{5^{2}+3^{2}} = \sqrt{34}$,即$OB^{2}+OA_{1}^{2} = A_{1}B^{2}$,
∴以$O$,$A_{1}$,$B$为顶点的三角形的形状为等腰直角三角形

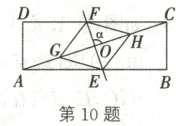
10. 如图,在矩形 $ ABCD $ 中,对角线 $ AC $ 的中点为 $ O $ 点,点 $ G $,$ H $ 在对角线 $ AC $ 上,$ AG = CH $,直线 $ GH $ 绕点 $ O $ 按逆时针方向旋转 $ \alpha $ 的角度,与边 $ AB $,$ CD $ 分别交于点 $ E $,$ F $(点 $ E $ 不与点 $ A $,$ B $ 重合)。
(1)求证:四边形 $ EHFG $ 是平行四边形;
(2)若 $ \alpha = 90^{\circ} $,$ AB = 9 $,$ AD = 3 $,求 $ AE $ 的长。
(1)求证:四边形 $ EHFG $ 是平行四边形;
(2)若 $ \alpha = 90^{\circ} $,$ AB = 9 $,$ AD = 3 $,求 $ AE $ 的长。

答案:
10.
(1)
∵对角线$AC$的中点为$O$,
∴$AO = CO$.
∵$AG = CH$,
∴$GO = HO$.
∵四边形$ABCD$是矩形,
∴$AD = BC$,$CD = AB$,$CD// AB$.
∴ $\angle FCO = \angle EAO$.
∵$\angle FOC = \angle EOA$,
∴$\triangle COF \cong \triangle AOE$.
∴$FO = EO$.
∴四边形$EHFG$是平行四边形
(2)如图,连接$CE$.
∵$\alpha = 90^{\circ}$,$EF \perp AC$,
∴$EF$是$AC$的垂直平分线.
∴$AE = CE$.
∵四边形$ABCD$是矩形,
∴$BC = AD = 3$.在$Rt\triangle BCE$中,$CE^{2} = BC^{2} + BE^{2}$,
∴$AE^{2} = 3^{2} + (9 - AE)^{2}$,
∴$AE = 5$

10.
(1)
∵对角线$AC$的中点为$O$,
∴$AO = CO$.
∵$AG = CH$,
∴$GO = HO$.
∵四边形$ABCD$是矩形,
∴$AD = BC$,$CD = AB$,$CD// AB$.
∴ $\angle FCO = \angle EAO$.
∵$\angle FOC = \angle EOA$,
∴$\triangle COF \cong \triangle AOE$.
∴$FO = EO$.
∴四边形$EHFG$是平行四边形
(2)如图,连接$CE$.
∵$\alpha = 90^{\circ}$,$EF \perp AC$,
∴$EF$是$AC$的垂直平分线.
∴$AE = CE$.
∵四边形$ABCD$是矩形,
∴$BC = AD = 3$.在$Rt\triangle BCE$中,$CE^{2} = BC^{2} + BE^{2}$,
∴$AE^{2} = 3^{2} + (9 - AE)^{2}$,
∴$AE = 5$

11. 如图,正方形 $ ABCD $ 内有一点 $ P $,且 $ PA = 1 $,$ PB = 2 $,$ PC = 3 $,则 $ \angle APB $ 的度数为
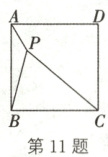
135^{\circ}
。
答案:
11.$135^{\circ}$
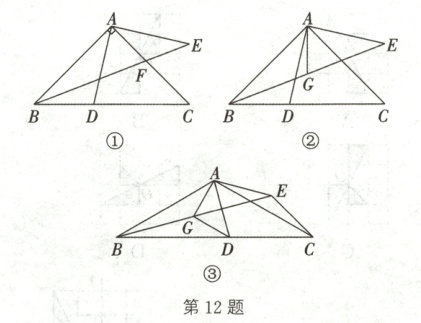
12. (重庆中考)在 $ \triangle ABC $ 中,$ AB = AC $,$ D $ 是边 $ BC $ 上一动点,连接 $ AD $,将 $ AD $ 绕点 $ A $ 按逆时针方向旋转至 $ AE $ 的位置,使得 $ \angle DAE + \angle BAC = 180^{\circ} $。
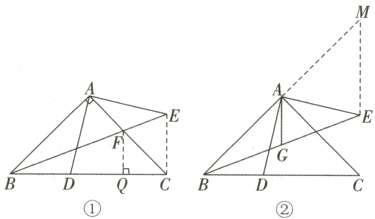
(1)如图①,当 $ \angle BAC = 90^{\circ} $ 时,连接 $ BE $,交 $ AC $ 于点 $ F $。若 $ BE $ 平分 $ \angle ABC $,$ BD = 2 $,求 $ AF $ 的长。
(2)如图②,取 $ BE $ 的中点 $ G $,连接 $ AG $。猜想 $ AG $ 与 $ CD $ 之间的数量关系,并证明你的猜想。
(3)如图③,在(2)的条件下,连接 $ DG $,$ CE $。若 $ \angle BAC = 120^{\circ} $,当 $ BD \gt CD $,$ \angle AEC = 150^{\circ} $ 时,请直接写出 $ \frac{BD - DG}{CE} $ 的值。
(1)如图①,当 $ \angle BAC = 90^{\circ} $ 时,连接 $ BE $,交 $ AC $ 于点 $ F $。若 $ BE $ 平分 $ \angle ABC $,$ BD = 2 $,求 $ AF $ 的长。
(2)如图②,取 $ BE $ 的中点 $ G $,连接 $ AG $。猜想 $ AG $ 与 $ CD $ 之间的数量关系,并证明你的猜想。
(3)如图③,在(2)的条件下,连接 $ DG $,$ CE $。若 $ \angle BAC = 120^{\circ} $,当 $ BD \gt CD $,$ \angle AEC = 150^{\circ} $ 时,请直接写出 $ \frac{BD - DG}{CE} $ 的值。

答案:
12.
(1)如图①,连接$CE$,过点$F$作$FQ \perp BC$于点$Q$.
∵$BE$平分$\angle ABC$,$\angle BAC = 90^{\circ}$,$FQ \perp BC$,
∴$FA = FQ$.
∵$AB = AC$,$\angle BAC = 90^{\circ}$,
∴$\angle ABC = \angle ACB = 45^{\circ}$.$\therefore \angle QFC = \angle QCF = 45^{\circ}$.$\therefore QF = QC$.$\therefore FC = \sqrt{QF^{2}+QC^{2}} = \sqrt{2FQ^{2}} = \sqrt{2}FQ$,即$FQ = \frac{\sqrt{2}}{2}FC$.$\because \angle DAE + \angle BAC = 180^{\circ}$,$\therefore \angle DAE = \angle BAC = 90^{\circ}$.$\therefore \angle BAC - \angle DAC = \angle DAE - \angle DAC$,即$\angle BAD = \angle CAE$.由旋转的性质,知$AD = AE$,
∴$\triangle ABD \cong \triangle ACE$.$\therefore BD = CE = 2$,$\angle ABD = \angle ACE = 45^{\circ}$.$\therefore \angle BCE = 90^{\circ}$.
∵$BE$平分$\angle ABC$,
∴$\angle ABF = \angle CBF$.
∴在$\triangle ABF$和$\triangle EBC$中,易得$\angle AFB = \angle BEC$.$\because \angle AFB = \angle CFE$,$\therefore \angle BEC = \angle CFE$.$\therefore CF = CE = 2$.$\therefore AF = FQ = \frac{\sqrt{2}}{2}FC = \sqrt{2}$
(2)$AG = \frac{1}{2}CD$ 如图②,延长$BA$至点$M$,使$AM = AB$,连接$EM$.$\because G$是$BE$的中点,
∴$AG = \frac{1}{2}ME$.$\because \angle BAC + \angle DAE = \angle BAC + \angle CAM = 180^{\circ}$,
∴$\angle DAE = \angle CAM$.$\therefore \angle DAE - \angle CAE = \angle CAM - \angle CAE$,即$\angle DAC = \angle EAM$.$\because AB = AM$,$AB = AC$,
∴$AC = AM$.由旋转的性质,知$AD = AE$,
∴$\triangle ADC \cong \triangle AEM$.$\therefore CD = ME$.$\therefore AG = \frac{1}{2}CD$
(3)$\frac{BD - DG}{CE} = \frac{\sqrt{6}}{2}$ 解析:如图③,延长$BA$至点$P$,使得$AP = AB$,连接$CP$,$EP$,$DE$.$\because \angle DAE + \angle BAC = 180^{\circ}$,$\angle BAC = 120^{\circ}$,$\therefore \angle DAE = 60^{\circ}$.又$\because AD = AE$,$\therefore \triangle ADE$是等边三角形.$\because AB = AC$,$\therefore \angle ACD = \frac{1}{2} × (180^{\circ} - 120^{\circ}) = 30^{\circ}$.$\because AC = AB = AP$,$\angle CAP = 180^{\circ} - \angle BAC = 60^{\circ}$,$\therefore \triangle ACP$是等边三角形.由(2),可知$\triangle ADC \cong \triangle AEP$,$\therefore \angle ACD = \angle APE = 30^{\circ}$.$\therefore PE$平分$\angle APC$.$\therefore PE$所在直线垂直平分线段$AC$.$\therefore AE = CE$.$\therefore \angle EAC = \angle ECA = \frac{1}{2}(180^{\circ} - \angle AEC) = 15^{\circ}$.$\therefore \angle CAD = \angle DAE - \angle EAC = 60^{\circ} - 15^{\circ} = 45^{\circ}$.$\therefore \angle ADB = \angle CAD + \angle ACD = 75^{\circ}$.易得$\angle BAD = 75^{\circ} = \angle ADB$.$\therefore BA = BD$.又$\because AE = DE$,$\therefore$易得$BE$垂直平分$AD$.$\therefore AG = DG$.设$BE$与$AC$交于点$H$,连接$DH$,则$AH = DH$,$\therefore$易得$\triangle AHD$是等腰直角三角形,即$\angle AHD = 90^{\circ}$.$\therefore \angle CHD = 180^{\circ} - \angle AHD = 90^{\circ}$.又$\because \angle DCH = 30^{\circ}$,$\therefore DH = \frac{1}{2}CD$.又由(2),可知$AG = \frac{1}{2}CD$,$\therefore AH = DH = AG = DG$.$\therefore$四边形$AGDH$是菱形.又$\because \angle AHD = 90^{\circ}$,$\therefore$四边形$AGDH$是正方形.设$AG = a$,则$CD = 2a$,$DG = AH = DH = a$,$\therefore$易得$CH = \sqrt{3}a$,$AD = \sqrt{2}a$.$\therefore BD = BA = AC = AH + HC = (1 + \sqrt{3})a$,$AD = AE = CE = \sqrt{2}a$.$\therefore \frac{BD - DG}{CE} = \frac{(1 + \sqrt{3})a - a}{\sqrt{2}a} = \frac{\sqrt{6}}{2}$.

12.
(1)如图①,连接$CE$,过点$F$作$FQ \perp BC$于点$Q$.
∵$BE$平分$\angle ABC$,$\angle BAC = 90^{\circ}$,$FQ \perp BC$,
∴$FA = FQ$.
∵$AB = AC$,$\angle BAC = 90^{\circ}$,
∴$\angle ABC = \angle ACB = 45^{\circ}$.$\therefore \angle QFC = \angle QCF = 45^{\circ}$.$\therefore QF = QC$.$\therefore FC = \sqrt{QF^{2}+QC^{2}} = \sqrt{2FQ^{2}} = \sqrt{2}FQ$,即$FQ = \frac{\sqrt{2}}{2}FC$.$\because \angle DAE + \angle BAC = 180^{\circ}$,$\therefore \angle DAE = \angle BAC = 90^{\circ}$.$\therefore \angle BAC - \angle DAC = \angle DAE - \angle DAC$,即$\angle BAD = \angle CAE$.由旋转的性质,知$AD = AE$,
∴$\triangle ABD \cong \triangle ACE$.$\therefore BD = CE = 2$,$\angle ABD = \angle ACE = 45^{\circ}$.$\therefore \angle BCE = 90^{\circ}$.
∵$BE$平分$\angle ABC$,
∴$\angle ABF = \angle CBF$.
∴在$\triangle ABF$和$\triangle EBC$中,易得$\angle AFB = \angle BEC$.$\because \angle AFB = \angle CFE$,$\therefore \angle BEC = \angle CFE$.$\therefore CF = CE = 2$.$\therefore AF = FQ = \frac{\sqrt{2}}{2}FC = \sqrt{2}$
(2)$AG = \frac{1}{2}CD$ 如图②,延长$BA$至点$M$,使$AM = AB$,连接$EM$.$\because G$是$BE$的中点,
∴$AG = \frac{1}{2}ME$.$\because \angle BAC + \angle DAE = \angle BAC + \angle CAM = 180^{\circ}$,
∴$\angle DAE = \angle CAM$.$\therefore \angle DAE - \angle CAE = \angle CAM - \angle CAE$,即$\angle DAC = \angle EAM$.$\because AB = AM$,$AB = AC$,
∴$AC = AM$.由旋转的性质,知$AD = AE$,
∴$\triangle ADC \cong \triangle AEM$.$\therefore CD = ME$.$\therefore AG = \frac{1}{2}CD$
(3)$\frac{BD - DG}{CE} = \frac{\sqrt{6}}{2}$ 解析:如图③,延长$BA$至点$P$,使得$AP = AB$,连接$CP$,$EP$,$DE$.$\because \angle DAE + \angle BAC = 180^{\circ}$,$\angle BAC = 120^{\circ}$,$\therefore \angle DAE = 60^{\circ}$.又$\because AD = AE$,$\therefore \triangle ADE$是等边三角形.$\because AB = AC$,$\therefore \angle ACD = \frac{1}{2} × (180^{\circ} - 120^{\circ}) = 30^{\circ}$.$\because AC = AB = AP$,$\angle CAP = 180^{\circ} - \angle BAC = 60^{\circ}$,$\therefore \triangle ACP$是等边三角形.由(2),可知$\triangle ADC \cong \triangle AEP$,$\therefore \angle ACD = \angle APE = 30^{\circ}$.$\therefore PE$平分$\angle APC$.$\therefore PE$所在直线垂直平分线段$AC$.$\therefore AE = CE$.$\therefore \angle EAC = \angle ECA = \frac{1}{2}(180^{\circ} - \angle AEC) = 15^{\circ}$.$\therefore \angle CAD = \angle DAE - \angle EAC = 60^{\circ} - 15^{\circ} = 45^{\circ}$.$\therefore \angle ADB = \angle CAD + \angle ACD = 75^{\circ}$.易得$\angle BAD = 75^{\circ} = \angle ADB$.$\therefore BA = BD$.又$\because AE = DE$,$\therefore$易得$BE$垂直平分$AD$.$\therefore AG = DG$.设$BE$与$AC$交于点$H$,连接$DH$,则$AH = DH$,$\therefore$易得$\triangle AHD$是等腰直角三角形,即$\angle AHD = 90^{\circ}$.$\therefore \angle CHD = 180^{\circ} - \angle AHD = 90^{\circ}$.又$\because \angle DCH = 30^{\circ}$,$\therefore DH = \frac{1}{2}CD$.又由(2),可知$AG = \frac{1}{2}CD$,$\therefore AH = DH = AG = DG$.$\therefore$四边形$AGDH$是菱形.又$\because \angle AHD = 90^{\circ}$,$\therefore$四边形$AGDH$是正方形.设$AG = a$,则$CD = 2a$,$DG = AH = DH = a$,$\therefore$易得$CH = \sqrt{3}a$,$AD = \sqrt{2}a$.$\therefore BD = BA = AC = AH + HC = (1 + \sqrt{3})a$,$AD = AE = CE = \sqrt{2}a$.$\therefore \frac{BD - DG}{CE} = \frac{(1 + \sqrt{3})a - a}{\sqrt{2}a} = \frac{\sqrt{6}}{2}$.


查看更多完整答案,请扫码查看


