《2025年通城学典非常课课通九年级数学上册人教版江苏专版》

10. 如图，AB 是⊙O 的直径，点 C 在⊙O 上，AD 垂直于过点 C 的切线，垂足为 D，CE⊥AB，垂足为 E。求证：CD = CE。

答案：
10.如图，连接AC,OC.
∵CD是⊙O的切线，
∴OC⊥CD.
∵AD⊥CD,
∴∠DCO=∠D=90°.
∴AD//OC.
∴∠DAC=∠ACO.
∵OC=OA,
∴∠ACO=∠CAO.
∴∠DAC=∠CAO.
∵CE⊥AB,CD⊥AD,
∴CD=CE

11. 如图，⊙O 为 Rt△ABC 的内切圆，切点分别为 D，E，F，且∠C = 90°，AB = 13，BC = 12。求：
（1）BF 的长；
（2）⊙O 的半径 r。

答案：
11.
(1)在Rt△ABC中，
∵∠C=90°,AB=13,BC=12,
∴AC=$\sqrt{AB^{2}-BC^{2}}$=$\sqrt{13^{2}-12^{2}}$=5.
∵⊙O为Rt△ABC的内切圆，切点分别为D,E,F，
∴BD=BF,AD=AE,CF=CE.设BF=BD=x,则AD=AE=13−x,CF=CE=12−x.
∵AE+EC=5,
∴13−x+12−x=5.
∴x=10.
∴BF=10　
(2)如图,连接OE,OF.
∵易知OE⊥AC,OF⊥BC,
∴∠OEC=∠C=∠OFC=90°.
∴四边形OECF是矩形.
∴OE=CF=BC−BF=12−10=2.
∴r=2

12. （玉林中考）如图，⊙O 与等边三角形 ABC 的边 AC，AB 分别交于点 D，E，AE 是直径，过点 D 作 DF⊥BC 于点 F。
（1）求证：DF 是⊙O 的切线；
（2）连接 EF，当 EF 是⊙O 的切线时，求⊙O 的半径 r 与等边三角形 ABC 的边长 a 之间的数量关系。

答案： 12.
(1)连接OD.
∵△ABC是等边三角形，
∴∠C=∠DAO=∠B=60°.
∵OD=OA,
∴△DOA是等边三角形.
∴∠ODA=∠C=60°.
∴OD//BC.
∴∠DFC=∠ODF.
∵DF⊥BC,
∴∠DFC=90°,
∴∠ODF=90°.
∴OD⊥DF.
∵OD是⊙O的半径,
∴DF是⊙O的切线
(2)由
(1),可知AD=r,则CD=a - r,BE=a - 2r.
∵在Rt△CFD中,∠C=60°,
∴∠CDF=30°.
∴CF=$\frac{1}{2}$CD=$\frac{1}{2}$(a - r).
∴BF=BC - CF=a - $\frac{1}{2}$(a - r)=$\frac{1}{2}$a + $\frac{1}{2}$r.又
∵EF是⊙O的切线，
∴FE⊥AB.
∴∠FEB=90°.在Rt△FEB中,∠B=60°,
∴∠EFB=30°.
∴BF=2BE.
∴$\frac{1}{2}$a + $\frac{1}{2}$r=2(a - 2r),解得a=3r,即r=$\frac{1}{3}$a.
∴⊙O的半径r与等边三角形ABC的边长a之间的数量关系为r=$\frac{1}{3}$a

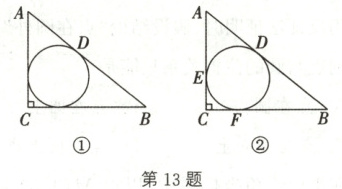
13. 有这样一个问题：如图①，Rt△ABC 的内切圆与斜边 AB 相切于点 D，AD = m，BD = n，求△ABC 的面积(用含 m，n 的式子表示)。
小冬根据学习几何的经验，先从特殊情况开始探究：
解：如图②，令 AD = 3，BD = 4，设△ABC 的内切圆分别与 AC，BC 相切于点 E，F，CE 的长为 x。根据切线长定理，得 AE = AD = 3，BF = BD = 4，CF = CE = x。根据勾股定理，得$(x + 3)^2 + (x + 4)^2 = (3 + 4)^2$。整理，得$x^2 + 7x = 12$。∴$S_{△ABC} = \frac{1}{2}AC·BC = \frac{1}{2}(x + 3)(x + 4) = \frac{1}{2}(x^2 + 7x + 12) = \frac{1}{2}×(12 + 12) = 12$。
请你参考小冬的做法，解决以下问题：
(1)当 AD = 5，BD = 7 时，求△ABC 的面积；
(2)当 AD = m，BD = n 时，△ABC 的面积为mn(用含 m，n 的式子表示)。

答案： 13.
(1)设△ABC的内切圆分别与AC,BC相切于点E，F,CE的长为x.根据切线长定理,得AE=AD=5,BF=BD=7,CF=CE=x.根据勾股定理,得(x + 5)$^{2}$+(x + 7)$^{2}$=(5 + 7)$^{2}$.整理,得x$^{2}$+12x=35.
∴$S_{\triangle ABC}$=$\frac{1}{2}$AC·BC=$\frac{1}{2}$(x + 5)(x + 7)=$\frac{1}{2}$(x$^{2}$+12x+35)=$\frac{1}{2}$×(35 + 35)=35
(2)mn 解析:设△ABC的内切圆分别与AC,BC相切于点E,F,CE的长为x.根据切线长定理，得AE=AD=m,BF=BD=n,CF=CE=x.根据勾股定理,得(x + m)$^{2}$+(x + n)$^{2}$=(m + n)$^{2}$.整理,得x$^{2}$+(m + n)x=mn.
∴$S_{\triangle ABC}$=$\frac{1}{2}$AC·BC=$\frac{1}{2}$(x + m)(x + n)=$\frac{1}{2}$[x$^{2}$+(m + n)x+mn]=$\frac{1}{2}$×(mn + mn)=mn.