2025年通城学典非常课课通九年级数学上册人教版江苏专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年通城学典非常课课通九年级数学上册人教版江苏专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. (2023·盐城)下列图形中,属于中心对称图形的是(
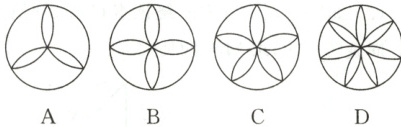
B
)
答案:
1.B
2. (2023·天津)如图,把△ABC以点A为中心按逆时针方向旋转得到△ADE,点B,C的对应点分别是D,E,且点E在BC的延长线上,连接BD,则下列结论一定正确的是(
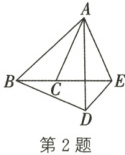
A.∠CAE=∠BED
B.AB=AE
C.∠ACE=∠ADE
D.CE=BD
A
)
A.∠CAE=∠BED
B.AB=AE
C.∠ACE=∠ADE
D.CE=BD
答案:
2.A
3. (2022·常德)如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C按顺时针方向旋转60°得到△DEC,点A,B的对应点分别是D,E,F是边AC的中点,连接BF,BE,FD.下列结论错误的是(
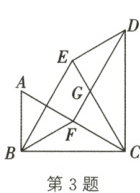
A.BE=BC
B.BF//DE,BF=DE
C.∠DFC=90°
D.DG=3GF
D
)
A.BE=BC
B.BF//DE,BF=DE
C.∠DFC=90°
D.DG=3GF
答案:
3.D
4. (2023·苏州一模)如图,点A的坐标为(-2,1),点B的坐标为(0,4),将线段AB绕点O按顺时针方向旋转得到对应线段A'B'.若点A'恰好落在x轴上,则点B'到x轴的距离为(
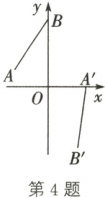
A.$\frac{4\sqrt{5}}{5}$
B.$\frac{8\sqrt{5}}{5}$
C.$\frac{3\sqrt{6}}{5}$
D.$\frac{8\sqrt{6}}{5}$
B
)
A.$\frac{4\sqrt{5}}{5}$
B.$\frac{8\sqrt{5}}{5}$
C.$\frac{3\sqrt{6}}{5}$
D.$\frac{8\sqrt{6}}{5}$
答案:
4.B
5. (2023·泗洪一模)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=4,将△ABC绕顶点C旋转得到△A'B'C.若O是BC的中点,P是A'B'的中点,在旋转过程中,线段OP长的最大值为(
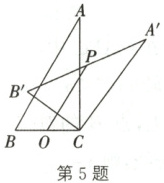
A.4
B.6
C.8
D.10
B
)
A.4
B.6
C.8
D.10
答案:
5.B
6. (2023·鼓楼模拟)如图,在平面直角坐标系中,点P的坐标为(0,2),点A的坐标为(4,2),以点P为旋转中心,把点A按逆时针方向旋转60°得到点B.在$M_1(-\frac{\sqrt{3}}{3},0)$,$M_2(-\sqrt{3},-1)$,$M_3(1,4)$,$M_4(2,\frac{11}{2})$四个点中,直线PB经过的点是(
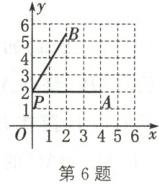
A.$M_1$
B.$M_2$
C.$M_3$
D.$M_4$
B
)
A.$M_1$
B.$M_2$
C.$M_3$
D.$M_4$
答案:
6.B 解析:
∵点A的坐标为(4,2),点P的坐标为(0,2),
∴PA⊥y轴,PA=4.由旋转得∠APB=60°,AP=PB=4.如图,过点B作BC⊥y轴于点C,
∴∠BPC=30°.
∴BC=2.
∴PC=2$\sqrt{3}$.
∴点B的坐标为(2,2+2$\sqrt{3}$).设直线PB对应的函数解析式为y=kx + b,则$\begin{cases}2k + b = 2 + 2\sqrt{3}, \\b = 2,\end{cases}$
∴$\begin{cases}k = \sqrt{3}, \\b = 2.\end{cases}$
∴直线PB对应的函数解析式为y=$\sqrt{3}$x+2.当y=0时,$\sqrt{3}$x+2=0,x=−$\frac{2\sqrt{3}}{3}$,
∴点M₁(−$\frac{2\sqrt{3}}{3}$,0)不在直线PB上.当x=−$\sqrt{3}$时,y=−3+2=−1,
∴点M₂(−$\sqrt{3}$,−1)在直线PB上.当x=1时,y=$\sqrt{3}$+2,
∴点M₃(1,4)不在直线PB上.当x=2时,y=2$\sqrt{3}$+2,
∴点M₄(2,$\frac{11}{2}$)不在直线PB上.

6.B 解析:
∵点A的坐标为(4,2),点P的坐标为(0,2),
∴PA⊥y轴,PA=4.由旋转得∠APB=60°,AP=PB=4.如图,过点B作BC⊥y轴于点C,
∴∠BPC=30°.
∴BC=2.
∴PC=2$\sqrt{3}$.
∴点B的坐标为(2,2+2$\sqrt{3}$).设直线PB对应的函数解析式为y=kx + b,则$\begin{cases}2k + b = 2 + 2\sqrt{3}, \\b = 2,\end{cases}$
∴$\begin{cases}k = \sqrt{3}, \\b = 2.\end{cases}$
∴直线PB对应的函数解析式为y=$\sqrt{3}$x+2.当y=0时,$\sqrt{3}$x+2=0,x=−$\frac{2\sqrt{3}}{3}$,
∴点M₁(−$\frac{2\sqrt{3}}{3}$,0)不在直线PB上.当x=−$\sqrt{3}$时,y=−3+2=−1,
∴点M₂(−$\sqrt{3}$,−1)在直线PB上.当x=1时,y=$\sqrt{3}$+2,
∴点M₃(1,4)不在直线PB上.当x=2时,y=2$\sqrt{3}$+2,
∴点M₄(2,$\frac{11}{2}$)不在直线PB上.

7. (2023·张家界)如图,AO为∠BAC的平分线,且∠BAC=50°,将四边形ABOC绕点A按逆时针方向旋转后,得到四边形AB'O'C',且∠OAC'=100°,则四边形ABOC旋转的角度是
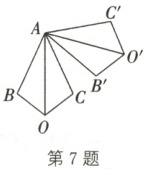
75°
.
答案:
7.75°
8. (2023·枣庄)银杏是著名的活化石植物,其叶有细长的叶柄,呈扇形.如图所示为一片银杏叶标本,叶片上点B,C的坐标分别为(-3,2),(4,3),将银杏叶绕原点按顺时针方向旋转90°后,叶柄上点A的对应点的坐标为
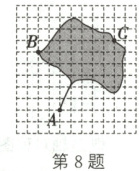
(−3,1)
.
答案:
8.(−3,1)
查看更多完整答案,请扫码查看


