《2025年通城学典非常课课通九年级数学上册人教版江苏专版》

1. 有下列方程：①$(x + 4)^2 = (x - 1)^2$；②$\frac{x^2}{3} + 5 = \frac{x}{2}$；③$\frac{2}{x^2} + \frac{1}{x} + 6 = 1$；④$x^2 - 7 = 0$。其中，属于一元二次方程的个数是(B)

A.1
B.2
C.3
D.4

答案： 1.B

2. 设$\alpha$，$\beta$是方程$x^2 + 2023x - 2 = 0$的两根，则$(\alpha^2 + 2023\alpha - 1)(2\beta^2 + 4046\beta + 2)$的值是(D)

A.1
B.3
C.4
D.6

答案： 2.D

3. 已知关于$x$的一元二次方程$(a - 4)x^2 + x + |a| - 4 = 0$的一个根是$x = 0$，则实数$a$的值为-4。

答案： 3. -4

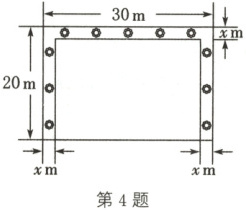
4. 学校计划在一块长$30m$、宽$20m$的矩形空地上划出四分之一的区域种花，小红同学的设计方案如图所示，求花带的宽度。设花带的宽度为$x m$，则可列方程为$(30 - 2x)(20 - x) = \frac{3}{4} × 20 × 30$。
]

答案： 4.$(30 - 2x)(20 - x) = \frac{3}{4} × 20 × 30$

5. 一个小组里共有$x$名同学，每名同学都分别给小组里的其他同学发一条信息，共发信息72条，则可列方程为$x(x - 1) = 72$。

答案： 5.$x(x - 1) = 72$

6. 已知方程$(m - 2)x^{m - 2} + (m + 1)x + 3m = 1$。
（1）如果该方程是关于$x$的一元二次方程，试确定$m$的值，并指出二次项系数、一次项系数及常数项；
（2）如果该方程是关于$x$的一元一次方程，试确定$m$的值。

答案： 6.
(1)由题意，得$m - 2 = 2$，$\therefore m = 4$。$\therefore$该方程为$2x^{2} + 5x + 11 = 0$。$\therefore$二次项系数是$2$，一次项系数是$5$，常数项是$11$
(2)由题意，得$\begin{cases}m - 2 = 1,\\m - 2 + m + 1 \neq 0\end{cases}$或$\begin{cases}m - 2 = 0,\\m + 1 \neq 0,\end{cases}$ $\therefore m = 3$或$m = 2$

7. 若关于$x$的一元二次方程$ax^2 + bx + 2 = 0(a \neq 0)$有一根为$x = 2021$，则一元二次方程$a(x + 1)^2 + bx + b = - 2$必有一根为$x = 2020$。

答案： 7.$x = 2020$

8. 定义：如果关于$x$的方程$a_1x^2 + b_1x + c_1 = 0(a_1 \neq 0,a_1,b_1,c_1$是常数)与$a_2x^2 + b_2x + c_2 = 0(a_2 \neq 0,a_2,b_2,c_2$是常数)，其中方程中的二次项系数、一次项系数、常数项分别满足$a_1 + a_2 = 0,b_1 = b_2,c_1 + c_2 = 0$，那么这两个方程互为“对称方程”。请用“对称方程”的定义解决下面的问题：
(1)方程$x^2 - 4x + 3 = 0$的“对称方程”是$-x^{2} - 4x - 3 = 0$；
(2)若关于$x$的方程$5x^2 + (m - 1)x - n = 0$与$-5x^2 - x = 1$互为“对称方程”，求$(m + n)^2$的值。

答案： 8.
(1)$-x^{2} - 4x - 3 = 0$
(2)由$-5x^{2} - x = 1$移项，可得$-5x^{2} - x - 1 = 0$。$\because$方程$5x^{2} + (m - 1)x - n = 0$与$-5x^{2} - x - 1 = 0$互为“对称方程”，$\therefore m - 1 = -1$，$-n + (-1) = 0$，解得$m = 0$，$n = -1$。$\therefore(m + n)^{2} = (0 - 1)^{2} = 1$