《2025年通城学典非常课课通九年级数学上册人教版江苏专版》

1. 一个图形经过平移或旋转，有下列说法：① 对应线段平行；② 对应线段相等；③ 对应角相等；④ 图形的形状和大小都没有发生变化。其中，一定正确的是(D)

A.①②③
B.①②④
C.①③④
D.②③④

答案： 1.D

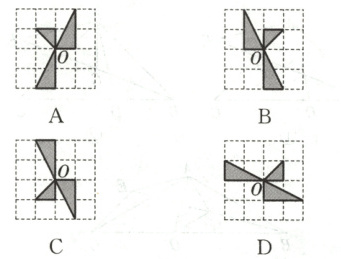
2. 如图，将方格纸中的图形绕点 $ O $ 按顺时针方向旋转 $ 90^{\circ} $，得到的图形是(B)

答案： 2.B

3. 如图，在平面直角坐标系中，其中一个三角形是由另一个三角形绕着某点旋转一定的角度得到的，则其旋转中心的坐标是(D)

A.$ (0,1) $
B.$ (0,2) $
C.$ (-1,1) $
D.$ (-1,2) $

答案： 3.D

4. (2023·荆州)如图，直线 $ y = -\frac{3}{2}x + 3 $ 分别与 $ x $ 轴、$ y $ 轴交于点 $ A $，$ B $，将 $ \triangle OAB $ 绕点 $ A $ 按顺时针方向旋转 $ 90^{\circ} $ 得到 $ \triangle CAD $，则点 $ B $ 的对应点 $ D $ 的坐标是(C)

A.$ (2,5) $
B.$ (3,5) $
C.$ (5,2) $
D.$ (\sqrt{13},2) $

答案： 4.C

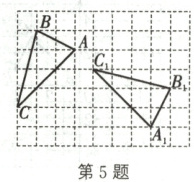
5. 如图，在正方形网格中，格点三角形 $ ABC $ 绕某点按顺时针方向旋转 $ \alpha (0^{\circ} \lt \alpha \lt 180^{\circ}) $ 得到格点三角形 $ A_1B_1C_1 $，$ A $ 与 $ A_1 $，$ B $ 与 $ B_1 $，$ C $ 与 $ C_1 $ 是对应点，则 $ \alpha = $90^{\circ}。

答案： 5.$90^{\circ}$

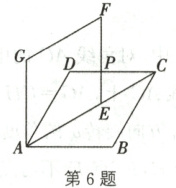
6. 如图，在菱形 $ ABCD $ 中，$ AB = 2 $，$ \angle BAD = 60^{\circ} $，将菱形 $ ABCD $ 绕点 $ A $ 按逆时针方向旋转，得到菱形 $ AEFG $，点 $ E $ 在 $ AC $ 上，$ EF $ 与 $ CD $ 交于点 $ P $，则 $ DP $ 的长是\sqrt{3}-1。

答案： 6.$\sqrt{3}-1$

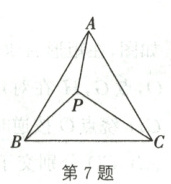
7. 如图，等边三角形 $ ABC $ 内有一点 $ P $，分别连接 $ AP $，$ BP $，$ CP $。若 $ AP = 6 $，$ BP = 8 $，$ CP = 10 $，则 $ S_{\triangle ABP} + S_{\triangle BPC} = $24 + 16\sqrt{3}。

答案： 7.$24 + 16\sqrt{3}$

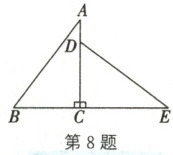
8. 如图，在 $ Rt \triangle ABC $ 中，$ \angle ACB = 90^{\circ} $，$ \triangle EDC $ 是由 $ \triangle ABC $ 绕点 $ C $ 按顺时针方向旋转得到的，且 $ B $，$ C $，$ E $ 三点在同一条直线上。
（1）求旋转角的度数；
（2）若 $ AB = 10 $，$ AC = 8 $，求 $ BE $ 的长。

答案： 8.
(1)由题意，得旋转角的度数为$90^{\circ}$　
(2)
∵$AB = 10$，$AC = 8$，$\angle ACB = 90^{\circ}$，
∴$BC = \sqrt{AB^{2}-AC^{2}} = 6$.由旋转的性质，得$CE = AC = 8$，
∴$BE = BC + CE = 6 + 8 = 14$