2025年通城学典非常课课通九年级数学上册人教版江苏专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年通城学典非常课课通九年级数学上册人教版江苏专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
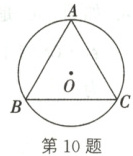
10. 如图,正三角形 ABC 的外接圆半径为 R。求正三角形 ABC 的边长、边心距、周长和面积。

答案:
10.连接OB,OC,过点O作OH⊥BC于点H.在Rt△OBH中$,OB = R,∠OBH=\frac{1}{2}∠ABC = 30^{\circ},$
∴$OH=\frac{1}{2}R,BH=\frac{\sqrt{3}}{2}R.$
∴$BC = 2BH=\sqrt{3}R.$
∴$C△ABC = 3BC = 3\sqrt{3}R,S△ABC = 3S△OBC = 3×\frac{1}{2}BC·$
$OH=\frac{3\sqrt{3}}{4}R^{2}.$
∴正三角形ABC的边长为$\sqrt{3}R,$边心距为$\frac{1}{2}R,$周长为$3\sqrt{3}R,$面积为$\frac{3\sqrt{3}}{4}R^{2}.$
∴$OH=\frac{1}{2}R,BH=\frac{\sqrt{3}}{2}R.$
∴$BC = 2BH=\sqrt{3}R.$
∴$C△ABC = 3BC = 3\sqrt{3}R,S△ABC = 3S△OBC = 3×\frac{1}{2}BC·$
$OH=\frac{3\sqrt{3}}{4}R^{2}.$
∴正三角形ABC的边长为$\sqrt{3}R,$边心距为$\frac{1}{2}R,$周长为$3\sqrt{3}R,$面积为$\frac{3\sqrt{3}}{4}R^{2}.$
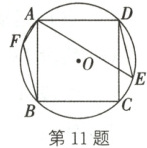
11. 如图,正方形 ABCD 内接于$\odot O$,E 为$\widehat{CD}$上任意一点(不与点 C,D 重合),连接 DE,AE。
(1)求$\angle AED$的度数。
(2)过点 B 作$BF// DE$,交$\odot O$于点 F,连接 AF。若$AF = 1$,$AE = 4$,求 DE 的长。
(1)求$\angle AED$的度数。
(2)过点 B 作$BF// DE$,交$\odot O$于点 F,连接 AF。若$AF = 1$,$AE = 4$,求 DE 的长。

答案:
11.
(1)连接OA,OD.
∵四边形ABCD是正方形且内接于⊙O,
∴$∠AOD = 90^{\circ}.$
∴$∠AED=\frac{1}{2}∠AOD = 45^{\circ}$
(2)连接CF,CE,CA,BD,过点D作DH⊥AE于点H.
∵BF//DE,AB//CD,
∴∠DBF = ∠BDE,∠ABD = ∠CDB.
∴∠BDE - ∠CDB = ∠DBF - ∠ABD,即∠CDE = ∠ABF.
∵$∠AFC = ∠ABC = 90^{\circ},∠ADC = ∠AEC = 90^{\circ},$
∴易得$∠DEC = ∠BFA = 135^{\circ}.$
∵CD = AB,
∴△CDE≌△ABF.
∴CE = AF = 1.在Rt△ACE中$,AC=\sqrt{AE^{2}+CE^{2}}=\sqrt{17}.$在Rt△ACD中,由勾股定理,易得$AD=\frac{\sqrt{34}}{2}.$
∵$∠DHE = 90^{\circ},∠HED = 45^{\circ}.$
∴DH = EH = x.设DH = EH = x,则AH = 4 - x.在Rt△ADH中$,AD^{2}=AH^{2}+DH^{2},$即$\frac{17}{2}=(4 - x)^{2}+x^{2},$解得$x_{1}=\frac{3}{2},x_{2}=\frac{5}{2}.$
∵E为CD上任意一点(不与点C,D重合),
∴$∠DAE < 45^{\circ}.$
∴DH < AH.
∴x < 4 - x,解得x < 2.
∴$x=\frac{3}{2}.$
∴易得$DE=\frac{3\sqrt{2}}{2}.$
(1)连接OA,OD.
∵四边形ABCD是正方形且内接于⊙O,
∴$∠AOD = 90^{\circ}.$
∴$∠AED=\frac{1}{2}∠AOD = 45^{\circ}$
(2)连接CF,CE,CA,BD,过点D作DH⊥AE于点H.
∵BF//DE,AB//CD,
∴∠DBF = ∠BDE,∠ABD = ∠CDB.
∴∠BDE - ∠CDB = ∠DBF - ∠ABD,即∠CDE = ∠ABF.
∵$∠AFC = ∠ABC = 90^{\circ},∠ADC = ∠AEC = 90^{\circ},$
∴易得$∠DEC = ∠BFA = 135^{\circ}.$
∵CD = AB,
∴△CDE≌△ABF.
∴CE = AF = 1.在Rt△ACE中$,AC=\sqrt{AE^{2}+CE^{2}}=\sqrt{17}.$在Rt△ACD中,由勾股定理,易得$AD=\frac{\sqrt{34}}{2}.$
∵$∠DHE = 90^{\circ},∠HED = 45^{\circ}.$
∴DH = EH = x.设DH = EH = x,则AH = 4 - x.在Rt△ADH中$,AD^{2}=AH^{2}+DH^{2},$即$\frac{17}{2}=(4 - x)^{2}+x^{2},$解得$x_{1}=\frac{3}{2},x_{2}=\frac{5}{2}.$
∵E为CD上任意一点(不与点C,D重合),
∴$∠DAE < 45^{\circ}.$
∴DH < AH.
∴x < 4 - x,解得x < 2.
∴$x=\frac{3}{2}.$
∴易得$DE=\frac{3\sqrt{2}}{2}.$
12. 周长是 12 的正三角形、正方形、正六边形的面积分别为$S_{3}$,$S_{4}$,$S_{6}$,三者之间的大小关系是(
A.$S_{6} > S_{4} > S_{3}$
B.$S_{3} > S_{4} > S_{6}$
C.$S_{6} > S_{3} > S_{4}$
D.$S_{4} > S_{6} > S_{3}$
A
)A.$S_{6} > S_{4} > S_{3}$
B.$S_{3} > S_{4} > S_{6}$
C.$S_{6} > S_{3} > S_{4}$
D.$S_{4} > S_{6} > S_{3}$
答案:
12.A
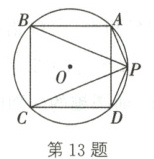
13. 如图,$\odot O$是边长为 1 的正方形 ABCD 的外接圆,P 是$\widehat{AD}$上的不同于点 A,D 的任意一点,则$PA^{2} + PB^{2} + PC^{2} + PD^{2}$的值为
4
。
答案:
13.4
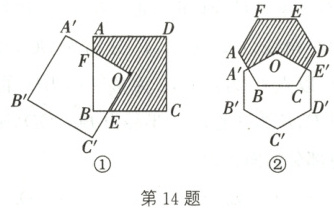
14. 如图①②所示分别为两个相同的正方形、正六边形,其中一个正多边形的顶点在另一个正多边形外接圆的圆心 O 处。求:
(1)图①中重叠部分与阴影部分的面积之比;
(2)图②中重叠部分与阴影部分的面积之比(直接写出答案)。
(1)图①中重叠部分与阴影部分的面积之比;
(2)图②中重叠部分与阴影部分的面积之比(直接写出答案)。

答案:
14.
(1)连接OA,OB.由题意,易得$∠AOB = ∠A′OC′ = 90^{\circ},AO = BO,∠OAF = ∠OBE = 45^{\circ},$
∴∠AOB - ∠BOF = ∠A′OC′ - ∠BOF,即∠AOF = ∠BOE.
∴△OAF≌△OBE.
∴S△OAF = S△OBE.
∴S四边形OEBF =
$S△OAB=\frac{1}{4}S$正方形ABCD.
∴S阴影 = S正方形ABCD - S四边形OEBF =
$\frac{3}{4}S$正方形ABCD.
∴S四边形OEBF:S阴影 = 1:3,即重叠部分与
阴影部分的面积之比为1:3
(2)1:2
(1)连接OA,OB.由题意,易得$∠AOB = ∠A′OC′ = 90^{\circ},AO = BO,∠OAF = ∠OBE = 45^{\circ},$
∴∠AOB - ∠BOF = ∠A′OC′ - ∠BOF,即∠AOF = ∠BOE.
∴△OAF≌△OBE.
∴S△OAF = S△OBE.
∴S四边形OEBF =
$S△OAB=\frac{1}{4}S$正方形ABCD.
∴S阴影 = S正方形ABCD - S四边形OEBF =
$\frac{3}{4}S$正方形ABCD.
∴S四边形OEBF:S阴影 = 1:3,即重叠部分与
阴影部分的面积之比为1:3
(2)1:2
查看更多完整答案,请扫码查看


