《2025年通城学典非常课课通九年级数学上册人教版江苏专版》

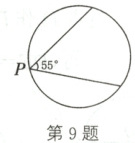
9. (2023·郴州)如图，某博览会上有一圆形展示区，在其圆形边缘的点P处安装了一台监视器，它的监控角度是55°，为了监控整个展示区，最少需要在圆形边缘上共安装这样的监视器4台.

答案： 9.4

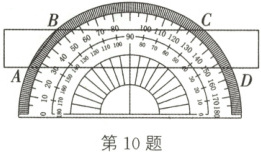
10. (2023·烟台)如图，将一个量角器与一把无刻度直尺水平摆放，直尺的长边与量角器的外弧分别交于点A，B，C，D，连接AB，则∠BAD的度数为52.5°.

答案： 10.52.5°

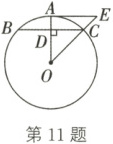
11. (2023·北京)如图，OA是⊙O的半径，BC是⊙O的弦，OA⊥BC于点D，AE是⊙O的切线，AE交OC的延长线于点E.若∠AOC=45°，BC=2，则线段AE的长为$\sqrt{2}$.

答案： 11.$\sqrt{2}$

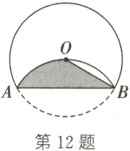
12. (2022·广元)如图，将⊙O沿弦AB折叠，$\overset{\frown}{AB}$恰好经过圆心O.若AB=2√{3}，则涂色部分的面积为$\frac{2}{3}π$.

答案： 12.$\frac{2}{3}π$

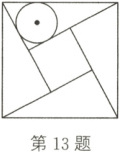
13. (2022·宜宾)如图，我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.若直角三角形的内切圆半径为3，小正方形的面积为49，则大正方形的面积为289.

答案： 13.289

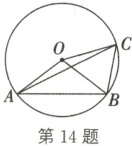
14. （2023·武汉）如图，OA，OB，OC都是⊙O的半径，∠ACB=2∠BAC.
（1）求证：∠AOB=2∠BOC；
（2）若AB=4，BC=√{5}，求⊙O的半径.

答案：
14.
(1)
∵$\widehat{AB} = \widehat{AB}$，
∴$\angle ACB = \frac{1}{2}\angle AOB$。
∵$\widehat{BC} = \widehat{BC}$，
∴$\angle BAC = \frac{1}{2}\angle BOC$。
∵$\angle ACB = 2\angle BAC$，
∴易得$\angle AOB = 2\angle BOC$。
(2)如图，过点$O$作$OD\perp AB$于点$E$，交⊙$O$于点$D$，连接$BD$，则$\angle DOB = \frac{1}{2}\angle AOB$，$AE = BE$。
∵$\angle AOB = 2\angle BOC$，
∴$\angle DOB = \angle BOC$。
∴$BD = BC$。
∵$AB = 4$，$BC = \sqrt{5}$，
∴$BE = 2$，$DB = \sqrt{5}$。在$Rt\triangle BDE$中，
∵$\angle DEB = 90^{\circ}$，
∴$DE = \sqrt{BD^{2} - BE^{2}} = 1$。在$Rt\triangle BOE$中，
∵$\angle OEB = 90^{\circ}$，
∴$OB^{2} = OE^{2} + BE^{2}$，即$OB^{2} = (OB - 1)^{2} + 2^{2}$。
∴$OB = \frac{5}{2}$，即⊙$O$的半径是$\frac{5}{2}$。
　　　　

15. （2023·临沂）如图，⊙O是△ABC的外接圆，BD是⊙O的直径，AB=AC，AE//BC，E为BD的延长线与AE的交点.
（1）求证：AE是⊙O的切线；
（2）若∠ABC=75°，BC=2，求$\overset{\frown}{CD}$的长.

答案：
15.
(1)如图，连接$AO$并延长，交$BC$于点$F$。
∵⊙$O$是$\triangle ABC$的外接圆，
∴$O$是$\triangle ABC$三边垂直平分线的交点。
∵$AB = AC$，
∴点$A$在线段$BC$的垂直平分线上。
∴易得$AO\perp BC$。
∵$AE// BC$，
∴$OA\perp AE$。
∵$OA$是⊙$O$的半径，
∴$AE$是⊙$O$的切线。
(2)如图，连接$OC$。
∵$AB = AC$，
∴$\angle ABC = \angle ACB = 75^{\circ}$。
∴$\angle BAC = 180^{\circ} - 2×75^{\circ} = 30^{\circ}$。
∴$\angle BOC = 2\angle BAC = 60^{\circ}$。
∵$OB = OC$，
∴$\triangle BOC$为等边三角形。
∴$OC = OB = BC = 2$。
∴$\angle COD = 180^{\circ} - \angle BOC = 120^{\circ}$。
∴$\widehat{CD}$的长为$\frac{120π×2}{180} = \frac{4π}{3}$。