2025年通城学典非常课课通九年级数学上册人教版江苏专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年通城学典非常课课通九年级数学上册人教版江苏专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
10. 如图,以$\triangle ABC$的边 BC 为直径作$\odot O$,点 A 在$\odot O$上,点 D 在 BC 的延长线上,$AD = AB$,$\angle D = 30^{\circ}$。
(1)求证:直线 AD 是$\odot O$的切线;
(2)若直径$BC = 4$,求图中涂色部分的面积。

(1)求证:直线 AD 是$\odot O$的切线;
(2)若直径$BC = 4$,求图中涂色部分的面积。

答案:
10.
(1)连接OA,则∠COA=2∠B.
∵AD=AB,
∴∠B=∠D=30°.
∴∠COA=60°.∠OAD=180° - 60° - 30°=90°.
∴OA⊥AD.
∵OA是⊙O的半径,
∴直线AD是⊙O的切线
(2)
∵BC=4,
∴OA=OC=2.在Rt△OAD中,∠D=30°,
∴OD=2OA=4.
∴AD=$\sqrt{OD^{2}-OA^{2}}=2\sqrt{3}$.
∴$S_{\triangle OAD}=\frac{1}{2}OA·AD=\frac{1}{2}×2×2\sqrt{3}=2\sqrt{3}$.
∵∠COA=60°,
∴$S_{扇形OAC}=\frac{60\pi×2^{2}}{360}=\frac{2\pi}{3}$.
∴$S_{涂色}=S_{\triangle OAD}-S_{扇形OAC}=2\sqrt{3}-\frac{2\pi}{3}$
(1)连接OA,则∠COA=2∠B.
∵AD=AB,
∴∠B=∠D=30°.
∴∠COA=60°.∠OAD=180° - 60° - 30°=90°.
∴OA⊥AD.
∵OA是⊙O的半径,
∴直线AD是⊙O的切线
(2)
∵BC=4,
∴OA=OC=2.在Rt△OAD中,∠D=30°,
∴OD=2OA=4.
∴AD=$\sqrt{OD^{2}-OA^{2}}=2\sqrt{3}$.
∴$S_{\triangle OAD}=\frac{1}{2}OA·AD=\frac{1}{2}×2×2\sqrt{3}=2\sqrt{3}$.
∵∠COA=60°,
∴$S_{扇形OAC}=\frac{60\pi×2^{2}}{360}=\frac{2\pi}{3}$.
∴$S_{涂色}=S_{\triangle OAD}-S_{扇形OAC}=2\sqrt{3}-\frac{2\pi}{3}$
11. 如图①,圆锥的母线长为 4 cm,圆锥的侧面展开图如图②所示,且$\angle AOA_{1} = 120^{\circ}$,一只蚂蚁欲从圆锥的底面上的点 A 出发,沿圆锥侧面爬行一周回到点 A。求蚂蚁需要爬行的最短路径的长。


答案:
11.连接AA₁,过点O作OE⊥AA₁于点E.
∵AO=A₁O,
∴∠AOE=$\frac{1}{2}$∠AOA₁=60°,AE=A₁E.
∴∠OAE=90° - 60°=30°. 在Rt△AOE中,OE=$\frac{1}{2}AO=2$ cm.
∴$AE=\sqrt{AO^{2}-OE^{2}}=2\sqrt{3}$ cm.
∴AA₁=2AE=4$\sqrt{3}$ cm.
∴蚂蚁需要爬行的最短路径的长为4$\sqrt{3}$ cm
∵AO=A₁O,
∴∠AOE=$\frac{1}{2}$∠AOA₁=60°,AE=A₁E.
∴∠OAE=90° - 60°=30°. 在Rt△AOE中,OE=$\frac{1}{2}AO=2$ cm.
∴$AE=\sqrt{AO^{2}-OE^{2}}=2\sqrt{3}$ cm.
∴AA₁=2AE=4$\sqrt{3}$ cm.
∴蚂蚁需要爬行的最短路径的长为4$\sqrt{3}$ cm
12. 如图,C 为半圆 O 内一点,点 O 为圆心,直径 AB 的长为 2 cm,$\angle BOC = 60^{\circ}$,$\angle BCO = 90^{\circ}$,将$\triangle BOC$绕圆心 O 按逆时针方向旋转至$\triangle B'OC'$处,点$C'$在 OA 上,则边 BC 扫过区域(涂色部分)的面积为

$\frac{1}{4}\pi$
$cm^{2}$。
答案:
12.$\frac{1}{4}\pi$
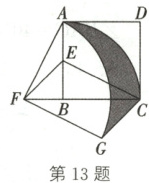
13. 如图,在正方形 ABCD 中,$AD = 2$,E 是 AB 的中点,将$\triangle BEC$绕点 B 按逆时针方向旋转$90^{\circ}$后,点 E 落在 CB 的延长线上的点 F 处,点 C 落在点 A 处。再将线段 AF 绕点 F 按顺时针方向旋转$90^{\circ}$得线段 GF,连接 EF,CG。
(1)求证:$EF// CG$;
(2)求点 C,A 在旋转过程中形成的$\overset{\frown}{AC}$,$\overset{\frown}{AG}$与线段 CG 所围成的涂色部分的面积。
(1)求证:$EF// CG$;
(2)求点 C,A 在旋转过程中形成的$\overset{\frown}{AC}$,$\overset{\frown}{AG}$与线段 CG 所围成的涂色部分的面积。

答案:
13.
(1)如图,
∵四边形ABCD是正方形,
∴AB=BC=AD=2,∠5=90°.
∵△BEC绕点B按逆时针方向旋转90°得△BFA,
∴△BFA≌△BEC.
∴∠1=∠3,∠4=∠5=90°,AF=CE.
∴∠AFB+∠1=90°.
∵线段AF绕点F按顺时针方向旋转90°得线段GF,
∴∠AFB+∠2=∠AFG=90°,AF=GF.
∴∠2=∠1=∠3.
∴CE//GF.
∵AF=CE,AF=GF,
∴CE=GF.
∴四边形EFGC是平行四边形.
∴EF//CG
(2)
∵E为AB的中点,
∴AE=BE.
∵由
(1),知△BFA≌△BEC,
∴BF=BE=$\frac{1}{2}AB=1$.
∴$AF=\sqrt{AB^{2}+BF^{2}}=\sqrt{5}$.在△FEC和△CGF中,EC=GF,∠3=∠2,FC=CF,
∴△FEC≌△CGF.
∴$S_{\triangle FEC}=S_{\triangle CGF}$.
∴$S_{涂色}=S_{扇形BAC}+S_{\triangle ABF}+S_{\triangle CGF}-S_{扇形FAG}=\frac{90\pi×2^{2}}{360}+\frac{1}{2}×2×1+\frac{1}{2}×(1 + 2)×1-\frac{90\pi×(\sqrt{5})^{2}}{360}=\frac{5}{2}-\frac{\pi}{4}$

13.
(1)如图,
∵四边形ABCD是正方形,
∴AB=BC=AD=2,∠5=90°.
∵△BEC绕点B按逆时针方向旋转90°得△BFA,
∴△BFA≌△BEC.
∴∠1=∠3,∠4=∠5=90°,AF=CE.
∴∠AFB+∠1=90°.
∵线段AF绕点F按顺时针方向旋转90°得线段GF,
∴∠AFB+∠2=∠AFG=90°,AF=GF.
∴∠2=∠1=∠3.
∴CE//GF.
∵AF=CE,AF=GF,
∴CE=GF.
∴四边形EFGC是平行四边形.
∴EF//CG
(2)
∵E为AB的中点,
∴AE=BE.
∵由
(1),知△BFA≌△BEC,
∴BF=BE=$\frac{1}{2}AB=1$.
∴$AF=\sqrt{AB^{2}+BF^{2}}=\sqrt{5}$.在△FEC和△CGF中,EC=GF,∠3=∠2,FC=CF,
∴△FEC≌△CGF.
∴$S_{\triangle FEC}=S_{\triangle CGF}$.
∴$S_{涂色}=S_{扇形BAC}+S_{\triangle ABF}+S_{\triangle CGF}-S_{扇形FAG}=\frac{90\pi×2^{2}}{360}+\frac{1}{2}×2×1+\frac{1}{2}×(1 + 2)×1-\frac{90\pi×(\sqrt{5})^{2}}{360}=\frac{5}{2}-\frac{\pi}{4}$

查看更多完整答案,请扫码查看


