2025年通城学典非常课课通九年级数学上册人教版江苏专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年通城学典非常课课通九年级数学上册人教版江苏专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
11. (随州中考)已知关于 $x$ 的一元二次方程 $x^{2}+(2m + 1)x + m - 2 = 0$.
(1)求证:无论 $m$ 取何值,此方程总有两个不等的实数根;
(2)若方程有两个实数根 $x_{1},x_{2}$,且 $x_{1}+x_{2}+3x_{1}x_{2}=1$,求 $m$ 的值.
(1)求证:无论 $m$ 取何值,此方程总有两个不等的实数根;
(2)若方程有两个实数根 $x_{1},x_{2}$,且 $x_{1}+x_{2}+3x_{1}x_{2}=1$,求 $m$ 的值.
答案:
(1) 依题意,得$Δ=(2m + 1)^{2}-4(m - 2)=4m^{2}+9>0,$
∴ 无论m取何值,此方程总有两个不等的实数根
(2) 由根与系数的关系,得$x_{1}+x_{2}=-(2m + 1),x_{1}x_{2}=m - 2. $
∵$ x_{1}+x_{2}+3x_{1}x_{2}=1,$
∴ -(2m + 1)+3(m - 2)=1,解得m=8
(1) 依题意,得$Δ=(2m + 1)^{2}-4(m - 2)=4m^{2}+9>0,$
∴ 无论m取何值,此方程总有两个不等的实数根
(2) 由根与系数的关系,得$x_{1}+x_{2}=-(2m + 1),x_{1}x_{2}=m - 2. $
∵$ x_{1}+x_{2}+3x_{1}x_{2}=1,$
∴ -(2m + 1)+3(m - 2)=1,解得m=8
12. (南充中考)已知关于 $x$ 的一元二次方程 $x^{2}-(2k + 1)x + k^{2}+k = 0$.
(1)求证:无论 $k$ 取何值,方程都有两个不等的实数根;
(2)若方程的两个实数根为 $x_{1},x_{2}$,且 $k$ 与 $\frac{x_{1}}{x_{2}}$ 都为整数,求 $k$ 所有可能的值.
(1)求证:无论 $k$ 取何值,方程都有两个不等的实数根;
(2)若方程的两个实数根为 $x_{1},x_{2}$,且 $k$ 与 $\frac{x_{1}}{x_{2}}$ 都为整数,求 $k$ 所有可能的值.
答案:
(1)
∵$ Δ=[-(2k + 1)]^{2}-4×1×(k^{2}+k)=1>0,$
∴ 无论k取何值,方程都有两个不等的实数根
(2) 方程$x^{2}-(2k + 1)x+k^{2}+k=0$可化为(x - k)[x - (k + 1)]=0,解得x=k或x=k + 1.
∴ 方程$x^{2}-(2k + 1)x+k^{2}+k=0$的两根为k,k + 1. ① 当$\frac{x_{1}}{x_{2}}=\frac{k}{k + 1}$时,$\frac{x_{1}}{x_{2}}=\frac{k + 1 - 1}{k + 1}=1-\frac{1}{k + 1} $
∵ k与$\frac{x_{1}}{x_{2}}$都为整数,
∴ k + 1=±1,解得k=0或k=-2. ② 当$\frac{x_{1}}{x_{2}}=\frac{k + 1}{k}$时,$\frac{x_{1}}{x_{2}}=1+\frac{1}{k}$
∵ k与$\frac{x_{1}}{x_{2}}$都为整数,
∴ k=±1. 综上所述,k所有可能的值为±1或0或-2
(1)
∵$ Δ=[-(2k + 1)]^{2}-4×1×(k^{2}+k)=1>0,$
∴ 无论k取何值,方程都有两个不等的实数根
(2) 方程$x^{2}-(2k + 1)x+k^{2}+k=0$可化为(x - k)[x - (k + 1)]=0,解得x=k或x=k + 1.
∴ 方程$x^{2}-(2k + 1)x+k^{2}+k=0$的两根为k,k + 1. ① 当$\frac{x_{1}}{x_{2}}=\frac{k}{k + 1}$时,$\frac{x_{1}}{x_{2}}=\frac{k + 1 - 1}{k + 1}=1-\frac{1}{k + 1} $
∵ k与$\frac{x_{1}}{x_{2}}$都为整数,
∴ k + 1=±1,解得k=0或k=-2. ② 当$\frac{x_{1}}{x_{2}}=\frac{k + 1}{k}$时,$\frac{x_{1}}{x_{2}}=1+\frac{1}{k}$
∵ k与$\frac{x_{1}}{x_{2}}$都为整数,
∴ k=±1. 综上所述,k所有可能的值为±1或0或-2
13. 用转化的数学思想,可以解一些新的特殊的方程.例如:一元三次方程 $x^{3}+x^{2}-2x = 0$,可以通过因式分解把它转化为 $x(x^{2}+x - 2)=0$,解方程 $x = 0$ 和 $x^{2}+x - 2 = 0$,可得方程 $x^{3}+x^{2}-2x = 0$ 的解.
(1)问题:方程 $x^{3}+x^{2}-2x = 0$ 的解是 $x_{1}=0,x_{2}=$
(2)拓展:用转化思想求方程 $\sqrt{2x + 3}=x$ 的解.
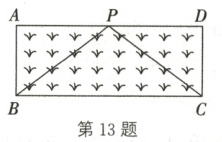
(3)应用:如图,矩形草坪 $ABCD$ 的长 $AD = 8m$,宽 $AB = 3m$,小华把一根长为 $10m$ 的绳子的一端固定在点 $B$,沿草坪边 $BA,AD$ 走到点 $P$ 处,把长绳 $PB$ 段拉直并固定在点 $P$ 处,然后沿草坪边 $PD,DC$ 走到点 $C$ 处,把长绳剩下的一段拉直,长绳的另一端恰好落在点 $C$ 处.求 $AP$ 的长.
(1)问题:方程 $x^{3}+x^{2}-2x = 0$ 的解是 $x_{1}=0,x_{2}=$
-2
,$x_{3}=$1
.(2)拓展:用转化思想求方程 $\sqrt{2x + 3}=x$ 的解.
(3)应用:如图,矩形草坪 $ABCD$ 的长 $AD = 8m$,宽 $AB = 3m$,小华把一根长为 $10m$ 的绳子的一端固定在点 $B$,沿草坪边 $BA,AD$ 走到点 $P$ 处,把长绳 $PB$ 段拉直并固定在点 $P$ 处,然后沿草坪边 $PD,DC$ 走到点 $C$ 处,把长绳剩下的一段拉直,长绳的另一端恰好落在点 $C$ 处.求 $AP$ 的长.

答案:
(1) -2 1
(2)
∵$ \sqrt{2x + 3}=x,$
∴$ 2x + 3=x^{2},$即$x^{2}-2x -3=0,$解得$x_{1}=3,x_{2}=-1. $当x=-1时,方程左边≠右边,
∴ x=-1不是原方程的解.当x=3时,方程左边=右边,
∴ x=3是原方程的解.
∴ 原方程的解为x=3
(3)
∵ 四边形ABCD是矩形,
∴ ∠A=∠D=90°,AB=CD=3m. 设AP=xm,则PD=(8 - x)m.
∴ 在Rt△ABP中,$BP=\sqrt{AB^{2}+AP^{2}}=\sqrt{9 + x^{2}}m;$在Rt△CDP中,$CP=\sqrt{PD^{2}+CD^{2}}=\sqrt{(8 - x)^{2}+9}m. $由题意,得BP + CP=10m,
∴$ \sqrt{9 + x^{2}}+\sqrt{(8 - x)^{2}+9}=10. $
∴$ \sqrt{(8 - x)^{2}+9}=10-\sqrt{9 + x^{2}}. $两边平方,得$(8 - x)^{2}+9=100 - 20\sqrt{9 + x^{2}}+9 + x^{2}. $整理,得$5\sqrt{9 + x^{2}}=4x + 9. $两边平方并整理,得$x^{2}-8x + 16=0,$解得$x_{1}=x_{2}=4.$经检验,x=4是原方程的解.
∴ AP的长为4m
(1) -2 1
(2)
∵$ \sqrt{2x + 3}=x,$
∴$ 2x + 3=x^{2},$即$x^{2}-2x -3=0,$解得$x_{1}=3,x_{2}=-1. $当x=-1时,方程左边≠右边,
∴ x=-1不是原方程的解.当x=3时,方程左边=右边,
∴ x=3是原方程的解.
∴ 原方程的解为x=3
(3)
∵ 四边形ABCD是矩形,
∴ ∠A=∠D=90°,AB=CD=3m. 设AP=xm,则PD=(8 - x)m.
∴ 在Rt△ABP中,$BP=\sqrt{AB^{2}+AP^{2}}=\sqrt{9 + x^{2}}m;$在Rt△CDP中,$CP=\sqrt{PD^{2}+CD^{2}}=\sqrt{(8 - x)^{2}+9}m. $由题意,得BP + CP=10m,
∴$ \sqrt{9 + x^{2}}+\sqrt{(8 - x)^{2}+9}=10. $
∴$ \sqrt{(8 - x)^{2}+9}=10-\sqrt{9 + x^{2}}. $两边平方,得$(8 - x)^{2}+9=100 - 20\sqrt{9 + x^{2}}+9 + x^{2}. $整理,得$5\sqrt{9 + x^{2}}=4x + 9. $两边平方并整理,得$x^{2}-8x + 16=0,$解得$x_{1}=x_{2}=4.$经检验,x=4是原方程的解.
∴ AP的长为4m
查看更多完整答案,请扫码查看


