2025年通城学典非常课课通九年级数学上册人教版江苏专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年通城学典非常课课通九年级数学上册人教版江苏专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
14. 一个三角形三边的长分别为 5,12,13,R 是其外接圆的半径,r 是其内切圆的半径,则 R-r 的值为(
A.4.5
B.3.5
C.5.5
D.2.5
A
)A.4.5
B.3.5
C.5.5
D.2.5
答案:
14.A
15. 马路上出现了三角形塌陷,数据如图所示,工人师傅想用一个圆形井盖把它覆盖,那么井盖的最小半径是

31.25
cm。
答案:
15.31.25
16. 如图,在△ABC 中,∠ACB = 90°,以 BC 为直径的⊙O 交 AB 于点 D,⊙O 的切线 DE 交 AC 于点 E,连接 CD。
(1)求证:E 是 AC 的中点;
(2)若 AB = 10,BC = 6,连接 OE,交 CD 于点 F,求 OF 的长。

(1)求证:E 是 AC 的中点;
(2)若 AB = 10,BC = 6,连接 OE,交 CD 于点 F,求 OF 的长。

答案:
16.
(1)
∵∠ACB=90°,BC为⊙O直径,
∴∠CDB=90°=∠ADC,AC是⊙O的切线.
∵ED切⊙O于点D,
∴EC=ED.
∴∠ECD=∠EDC.
∵∠A+∠ECD=∠ADE+∠EDC=90°,
∴∠A=∠ADE.
∴AE=ED.
∴AE=EC,即E是AC的中点
(2)如图,连接OD.
∵AC为⊙O的切线,DE是⊙O的切线,
∴EO平分∠CED.
∴OE⊥CD,F为CD的中点.
∵E,O分别为AC,BC的中点,
∴OE=$\frac{1}{2}$AB=$\frac{1}{2}$×10=5.在Rt△ACB 中,AB=10,BC=6,由勾股定理,得AC=8.
∵在Rt△ADC中,E为AC的中点,
∴DE=$\frac{1}{2}$AC=$\frac{1}{2}$×8=4.
∵BC=6,
∴DO=3.
∵$S_{\triangle EDO}$=$\frac{1}{2}$DE·DO=$\frac{1}{2}$OE·DF,
∴DF=$\frac{DE· DO}{OE}$=$\frac{4×3}{5}$=2.4.在Rt△DFO中,由勾股定理,得OF=$\sqrt{OD^{2}-DF^{2}}$=$\sqrt{3^{2}-2.4^{2}}$=1.8

16.
(1)
∵∠ACB=90°,BC为⊙O直径,
∴∠CDB=90°=∠ADC,AC是⊙O的切线.
∵ED切⊙O于点D,
∴EC=ED.
∴∠ECD=∠EDC.
∵∠A+∠ECD=∠ADE+∠EDC=90°,
∴∠A=∠ADE.
∴AE=ED.
∴AE=EC,即E是AC的中点
(2)如图,连接OD.
∵AC为⊙O的切线,DE是⊙O的切线,
∴EO平分∠CED.
∴OE⊥CD,F为CD的中点.
∵E,O分别为AC,BC的中点,
∴OE=$\frac{1}{2}$AB=$\frac{1}{2}$×10=5.在Rt△ACB 中,AB=10,BC=6,由勾股定理,得AC=8.
∵在Rt△ADC中,E为AC的中点,
∴DE=$\frac{1}{2}$AC=$\frac{1}{2}$×8=4.
∵BC=6,
∴DO=3.
∵$S_{\triangle EDO}$=$\frac{1}{2}$DE·DO=$\frac{1}{2}$OE·DF,
∴DF=$\frac{DE· DO}{OE}$=$\frac{4×3}{5}$=2.4.在Rt△DFO中,由勾股定理,得OF=$\sqrt{OD^{2}-DF^{2}}$=$\sqrt{3^{2}-2.4^{2}}$=1.8

17. 如图,在平面直角坐标系中,以点 O 为圆心,2 为半径的圆与 y 轴的正半轴交于点 A,P(4,2)是⊙O 外一点,直线 PB 与⊙O 相切于点 B,交 x 轴于点 C,连接 AP,AB。
(1)求证:PA 是⊙O 的切线;
(2)求点 B 的坐标;
(3)求直线 AB 对应的函数解析式。
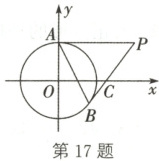
(1)求证:PA 是⊙O 的切线;
(2)求点 B 的坐标;
(3)求直线 AB 对应的函数解析式。

答案:
17.
(1)由题意,知点A的坐标为(0,2).
∵点P的坐标为(4,2),
∴AP//x轴.
∴AP⊥OA.又
∵OA是⊙O的半径,
∴PA是⊙O的切线
(2)连接OP,OB,过点P作PE⊥x轴于点E,则PE=2,过点B作BD⊥x轴于点D.
∵PB切⊙O于点B,
∴∠OBC=90°.
∵PE⊥OE,
∴∠OBC=∠PEC=90°.又
∵∠OCB=∠PCE,OB=PE=2,
∴△OBC≌△PEC.
∴BC=EC,OC=PC.设OC=PC=x.
∵易知OE=AP=4,
∴CE=OE−OC=4−x.在Rt△PCE中,
∵PC$^{2}$=CE$^{2}$+PE$^{2}$,
∴x$^{2}$=(4−x)$^{2}$+2$^{2}$,解得x=$\frac{5}{2}$.
∴BC=CE=4−$\frac{5}{2}$=$\frac{3}{2}$.
∵$\frac{1}{2}$OB·BC=$\frac{1}{2}$OC·BD,即$\frac{1}{2}$×2×$\frac{3}{2}$=$\frac{1}{2}$×$\frac{5}{2}$BD,
∴BD=$\frac{6}{5}$.
∴在Rt△OBD中,OD=$\sqrt{OB^{2}-BD^{2}}$=$\frac{8}{5}$.
∵点B在第四象限,
∴点B的坐标为($\frac{8}{5}$,-$\frac{6}{5}$)
(3)设直线AB对应的函数解析式为y=kx + b.把A(0,2),B($\frac{8}{5}$,-$\frac{6}{5}$)代入,得$\begin{cases}b=2\frac{8}{5}k + b=-\frac{6}{5}\end{cases}$,解得$\begin{cases}k=-2\\b=2\end{cases}$
∴直线AB对应的函数解析式为y=-2x + 2
(1)由题意,知点A的坐标为(0,2).
∵点P的坐标为(4,2),
∴AP//x轴.
∴AP⊥OA.又
∵OA是⊙O的半径,
∴PA是⊙O的切线
(2)连接OP,OB,过点P作PE⊥x轴于点E,则PE=2,过点B作BD⊥x轴于点D.
∵PB切⊙O于点B,
∴∠OBC=90°.
∵PE⊥OE,
∴∠OBC=∠PEC=90°.又
∵∠OCB=∠PCE,OB=PE=2,
∴△OBC≌△PEC.
∴BC=EC,OC=PC.设OC=PC=x.
∵易知OE=AP=4,
∴CE=OE−OC=4−x.在Rt△PCE中,
∵PC$^{2}$=CE$^{2}$+PE$^{2}$,
∴x$^{2}$=(4−x)$^{2}$+2$^{2}$,解得x=$\frac{5}{2}$.
∴BC=CE=4−$\frac{5}{2}$=$\frac{3}{2}$.
∵$\frac{1}{2}$OB·BC=$\frac{1}{2}$OC·BD,即$\frac{1}{2}$×2×$\frac{3}{2}$=$\frac{1}{2}$×$\frac{5}{2}$BD,
∴BD=$\frac{6}{5}$.
∴在Rt△OBD中,OD=$\sqrt{OB^{2}-BD^{2}}$=$\frac{8}{5}$.
∵点B在第四象限,
∴点B的坐标为($\frac{8}{5}$,-$\frac{6}{5}$)
(3)设直线AB对应的函数解析式为y=kx + b.把A(0,2),B($\frac{8}{5}$,-$\frac{6}{5}$)代入,得$\begin{cases}b=2\frac{8}{5}k + b=-\frac{6}{5}\end{cases}$,解得$\begin{cases}k=-2\\b=2\end{cases}$
∴直线AB对应的函数解析式为y=-2x + 2
查看更多完整答案,请扫码查看


