《2025年1加1轻巧夺冠完美期末八年级数学上册北师大版辽宁专版》

23. （13分）（沈阳和平期末）
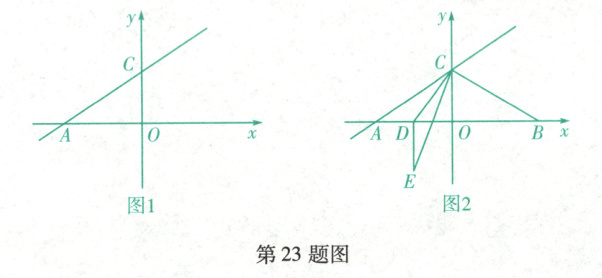
如图，一次函数$y = \frac{\sqrt{3}}{3}x + 3$，与$x$轴交于点$A$，与$y$轴交于点$C$，点$B$在$x$轴正半轴，$OB = \sqrt{3}OC$.
(1)求点$C$的坐标与直线$BC$的表达式.
(2)直线$AC$上是否存在一点$P$，使得$S_{\triangle AOP} = 3\sqrt{3}$？若存在，求出点$P$的坐标；若不存在，请说明理由.
(3)$D$是$\triangle ABC$的边$AB$上一动点（不与点$A$，$B$重合），将$\triangle ACD$沿$CD$所在直线折叠，点$A$的对应点为$E$. 若$DE$所在的直线与$\triangle ABC$的一边垂直，求点$D$的坐标.

答案：
23.解：
(1)一次函数$y = \frac{\sqrt{3}}{3}x + 3$，与x轴交于点A，与y轴交于点C，则点A，C的坐标分别为A( - $3\sqrt{3}$，0)，C(0，3)，则$OB = \sqrt{3}OC = \sqrt{3} × 3 = 3\sqrt{3} = OA$，故直线AC和直线BC关于y轴对称，则直线BC的表达式为$y = - \frac{\sqrt{3}}{3}x + 3$。
(2)
∵$S_{\triangle AOP} = \frac{1}{2}AO · |y_P| = \frac{1}{2} × 3\sqrt{3} × |y_P| = 3\sqrt{3}$，则$y_P = \pm 2 = \frac{\sqrt{3}}{3}x + 3$，解得$x_P = - \sqrt{3}$或$x_P = - 5\sqrt{3}$，故点P的坐标为( - $\sqrt{3}$，2)或( - $5\sqrt{3}$， - 2)。
(3)由
(1)知$AO = 3\sqrt{3}$，OC = 3，则$AC = 6$，则∠CAO = 30° = ∠ABC，分三种情况：①当DE⊥AB时，如答图1，设CE与x轴交于点H，则∠E = ∠CAO = 30°，则∠CHO = ∠DHE = 90° - 30° = 60°。在Rt△CHO中，∠CHO = 60°，CO = 3，设OH = a，则CH = 2a，OC = $\sqrt{3}a = 3$，解得a = $\sqrt{3} = OH$。设DH = x，则$HE = 2x$，DE = $\sqrt{3}x$ = AD，则$AO = 3\sqrt{3} = AD + DH + OH = (\sqrt{3} + 1)x + \sqrt{3}$，解得x = $3 - \sqrt{3}$，则OD = x + OH = 3，故点D的坐标为( - 3，0)；②当DE⊥BC时，如答图2，则∠EDB = 90° - 30° = 60°，而∠CDE = ∠CDO = $\frac{1}{2}(180° - ∠EDB) = 60°$，即点D和①中的点H关于y轴对称，故点D的坐标为(3，0)；③当DE⊥AC时，如答图3，延长ED交AC于点H，
∵DH⊥AC，则∠HDA = 90° - 30° = 60° = ∠ODE，而∠DEO = 30°，则∠DOE = 90°，即点E在y轴负半轴上。设OD = x = DH，则AD = DE = 2x，则AO = AD + OD = 3x = $3\sqrt{3}$，解得x = $\sqrt{3}$，故点D的坐标为( - $\sqrt{3}$，0)。
综上所述，点D的坐标为( - 3，0)或(3，0)或( - $\sqrt{3}$，0)。