《2025年1加1轻巧夺冠完美期末八年级数学上册北师大版辽宁专版》

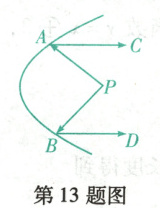
13. (丹东期末) 如图是某灯具的镜面反射示意图,从光源点$P$处发出的光线$PA$,$PB$经弯曲的镜面反射后射出,且满足反射光线$AC// BD$.若$\angle PAC=40^{\circ}$,$PA\perp PB$于点$P$,则$\angle PBD$的度数为50°.

答案： 50°

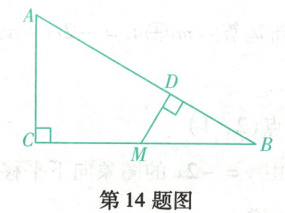
14. (沈阳法库期末) 在$\triangle ABC$中,$\angle C=90^{\circ}$,$M$是$BC$的中点,$MD\perp AB$于点$D$.若$AC=2$ cm,$AD=\frac{5}{2}$ cm,则$BD$的长为$\frac{3}{2}$ cm.

答案：
$\frac{3}{2}$　[解析]连接AM，如答图，设BD=x，BM=y，MD=a，
∵M是BC的中点，
∴CM=BM=y，
∵∠C=90°，MD⊥AB于点D，
∴△ACM，△ADM，△BDM均为直角三角形，在Rt△ACM中，由勾股定理得AM²=AC²+CM²=2²+y²=4 + y²，在Rt△ADM中，由勾股定理得AM²=AD²+MD²=($\frac{5}{2}$)²+a²=$\frac{25}{4}$+a²，
∴$\frac{25}{4}$+a²=4 + y²，在Rt△BDM中，由勾股定理得MD²=BM²−BD²，即a²=y²−x²，
∴$\frac{25}{4}$+y²−x²=4 + y²，整理得x²=$\frac{9}{4}$，解得x₁=$\frac{3}{2}$，x₂=−$\frac{3}{2}$(不合题意，舍去)，
∴BD的长为$\frac{3}{2}$cm。

15. (锦州期末) 在平面直角坐标系$xOy$中,$A$是$x$轴上一点,以原点$O$为圆心,$OA$的长为半径作弧交$y$轴于点$B$,再分别以点$A$,$B$为圆心,大于$\frac{1}{2}AB$的长为半径作弧,两弧交于点$C$.若点$C$的坐标为$(2a-2,10-a)$,则$a$的值为4或−8.

答案： 4或−8　[解析]由作法可知，OC为∠AOB的平分线，
∴∠AOC=45°，若点C的坐标为(2a −2,10−a)，在第一、三象限，有2a−2=10 −a，解得a=4；若点C(2a−2,10−a)在第二、四象限，有2a−2+10−a=0，解得a=−8。综上所述，a的值为4或−8。

16. (每小题5分,共10分)(沈阳铁西期末)
(1)计算:$\sqrt{\frac{25}{2}}+\sqrt{32}-\sqrt{27}×\sqrt{3}$;
(2)解方程组:$\begin{cases}2x+y=28,\\x+2y=26.\end{cases}$

答案： 16.解:
(1)原式=$\frac{5\sqrt{2}}{2}$+4$\sqrt{2}$−$\sqrt{27}$×3=$\frac{5\sqrt{2}}{2}$+4$\sqrt{2}$−9=$\frac{13\sqrt{2}}{2}$−9。
(2)$\begin{cases}2x + y=28①,\\x + 2y=26②,\end{cases}$①×2 - ②，得3x=56 - 26，解得x=10，把x=10代入①，得20 + y=28，解得y=8，所以原方程组的解为$\begin{cases}x=10,\\y=8.\end{cases}$

17. (8分)(沈阳沈河期末)
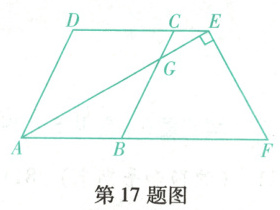
如图,$DC// AB$,点$E$,$F$分别在$DC$,$AB$的延长线上,$\angle DCB=\angle DAB$,$\angle AGB=30^{\circ}$,$\angle AFE=60^{\circ}$,$AE$平分$\angle DAB$.
(1)$AD$是否平行于$BC$?请说明理由.
(2)试说明$AE\perp EF$.

答案： 17.解:
(1)AD//BC，理由如下:
∵DC//AB，
∴∠DCB + ∠ABC=180°，
∵∠DCB=∠DAB，
∴∠DAB + ∠ABC=180°，
∴AD//BC。
(2)
∵AE平分∠DAB，
∴∠EAF=$\frac{1}{2}$∠DAB，
∵∠AGB=30°，
∴$\frac{1}{2}$∠DAB=∠ABC=180°−30°=150°，又
∵∠DAB + ∠ABC=180°，
∴$\frac{1}{2}$∠DAB =30°，即∠EAF=30°，
∴∠AEF=180°−∠EAF −∠AFE=90°，即AE⊥EF。