《2025年1加1轻巧夺冠完美期末八年级数学上册北师大版辽宁专版》

12. (朝阳建平期末)若关于$x$，$y$的方程组$\begin{cases}2x + 3y = 4, \\ 3x + 2y = 2m - 3\end{cases}$的解满足$x + y = \frac{3}{5}$，则$m$的值是 ______ .

答案： 12.1　[解析]$\begin{cases}2x + 3y = 4 & ① \\3x + 2y = 2m - 3 & ②\end{cases}$，① + ②，得5(x + y) = 2m + 1，解得$x + y = \frac{2m + 1}{5}$。代入$x + y = \frac{3}{5}$得$\frac{2m + 1}{5} = \frac{3}{5}$，解得m = 1。

13. (辽阳期末)如图，点$A$，$B$，$C$都在方格纸的格点上，若点$A$的坐标为$(-1,1)$，点$B$的坐标为$(1,-1)$，则点$C$的坐标是(1, 0).

答案：
13.(1, 0)　[解析]点A的坐标为( - 1, 1)，点B的坐标为(1, - 1)，由点的坐标建立平面直角坐标系xOy如答图，则点C的坐标是(1, 0)。

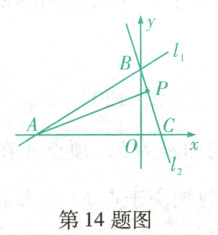
14. (沈阳大东期末)如图，直线$l_1: y = \frac{5}{12}x + 5$交$x$轴于点$A$，交$y$轴于点$B$，直线$l_2: y = -5x + 5$交$x$轴于点$C$，交$y$轴于点$B$，点$P$在线段$BC$上，且点$P$到$l_1$的距离是2，则点$P$的坐标是(\frac{2}{5}, 3).

答案： 14.$(\frac{2}{5}, 3)$　[解析]
∵直线$l_1$：$y = \frac{5}{12}x + 5$交x轴于点A，交y轴于点B，直线$l_2$：$y = - 5x + 5$交x轴于点C，交y轴于点B，
∴可求得三点坐标为A( - 12, 0)，B(0, 5)，C(1, 0)。
∴OA = 12，OC = 1，OB = 5，
∴$AB = \sqrt{12^2 + 5^2} = 13$，$AC = 12 + 1 = 13$。
∴$S_{\triangle ABC} = \frac{1}{2} × 13 × 5 = \frac{65}{2}$。
∵点P到$l_1$的距离是2，
∴$S_{\triangle APB} = \frac{1}{2} × 13 × 2 = 13$，
∴$S_{\triangle APC} = \frac{1}{2}AC · y_P = S_{\triangle ABC} - S_{\triangle APB} = \frac{65}{2} - 13 = \frac{39}{2}$，即$\frac{1}{2} × 13 × y_P = \frac{39}{2}$，解得$y_P = 3$。代入y = - 5x + 5，得3 = - 5x + 5，解得x = $\frac{2}{5}$。
∴点P的坐标是$(\frac{2}{5}, 3)$。

15. (沈阳沈河期末)如图，$M$，$N$分别为锐角$\angle AOB$边$OA$，$OB$上的点，把$\angle AOB$沿$MN$折叠，点$O$落在$\angle AOB$所在平面内的点$C$处. 若折叠后，直线$CM$与$OB$交于点$E$，且$MC \perp OB$，垂足为$E$，且$OM = 10$，$ME = 6$，则此时$ON$的长是5或20.

答案：
15.5或20　[解析]若折叠后，直线MC⊥OB于点E，
∵OM = 10，ME = 6，
∴$OE = \sqrt{OM^2 - ME^2} = 8$。分两种情况：①若点N在线段OE上，如答图1，由折叠的性质知CM = OM = 10，CN = ON，
∴CE = CM - EM = 10 - 6 = 4。在Rt△CEN中，EN = OE - ON = 8 - ON，由勾股定理得$EN^2 + CE^2 = CN^2$，即$(8 - ON)^2 + 4^2 = ON^2$，解得ON = 5；②若点N在线段OE的延长线上，如答图2，由折叠的性质知CM = OM = 10，CN = ON，
∴CE = CM + EM = 10 + 6 = 16。在Rt△CEN中，EN = ON - OE = ON - 8，由勾股定理得$EN^2 + CE^2 = CN^2$，即$(ON - 8)^2 + 16^2 = ON^2$，解得ON = 20。综上所述，ON的长是5或20。 　　　

16. （每小题5分，共10分）（沈阳浑南期末）
计算：
(1)$\sqrt[3]{8} - \sqrt{4} - \sqrt{(-3)^2} + |1 - \sqrt{2}|$；
(2)$(\sqrt{6} - 2\sqrt{5}) × \sqrt{3} - 6\sqrt{\frac{1}{2}}$.

答案： 16.解：
(1)原式 = $\sqrt{2} - 2 - 3 + \sqrt{2} - 1 = \sqrt{2} - 4$。
(2)原式 = $\sqrt{6} × \sqrt{3} - 2\sqrt{5} × \sqrt{3} - 3\sqrt{2} = 3\sqrt{2} - 2\sqrt{15} - 3\sqrt{2} = - 2\sqrt{15}$。

17. （8分）（沈阳铁西期末）
列二元一次方程组解应用题.
小明早上骑自行车上学，中途因道路施工步行了一段路，到学校共用20分钟. 他骑自行车的平均速度是200米/分，步行的平均速度是70米/分，他从家到学校的路程是3350米. 求小明骑自行车和步行的时间分别为多少分钟.

答案： 17.解：设小明骑自行车的时间为x分钟，步行的时间为y分钟，根据题意得$\begin{cases}x + y = 20 \\200x + 70y = 3350\end{cases}$，解得$\begin{cases}x = 15 \\y = 5\end{cases}$。
答：小明骑自行车的时间为15分钟，步行的时间为5分钟。