2025年1加1轻巧夺冠完美期末八年级数学上册北师大版辽宁专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年1加1轻巧夺冠完美期末八年级数学上册北师大版辽宁专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
22.(12 分)
在长方形$ABCD$中,$AB = 2$,$BC > AB$,$P$,$Q$分别是边$AD$,$BC$上的点,将四边形$APQB$沿$PQ$翻折,$A$,$B$两点的对应点分别为$F$,$E$.
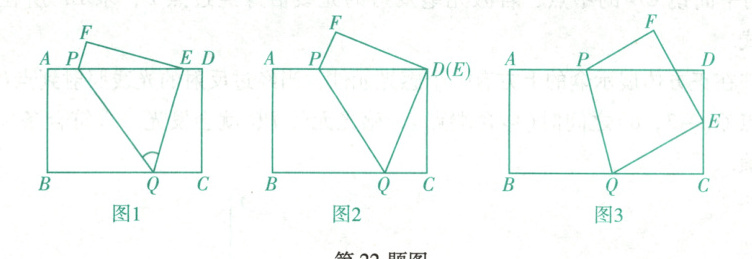
(1)如图 1,当点$E$落在$AD$上,求证:$PE = QE$.
(2)如图 2,若$BC = 3$,点$E$与点$D$重合,求$AP$的长.
(3)如图 3,若$\frac{AP}{BQ}=\frac{3}{4}$,点$E$恰好落在$CD$的中点处,求$BC$的长.
在长方形$ABCD$中,$AB = 2$,$BC > AB$,$P$,$Q$分别是边$AD$,$BC$上的点,将四边形$APQB$沿$PQ$翻折,$A$,$B$两点的对应点分别为$F$,$E$.
(1)如图 1,当点$E$落在$AD$上,求证:$PE = QE$.
(2)如图 2,若$BC = 3$,点$E$与点$D$重合,求$AP$的长.
(3)如图 3,若$\frac{AP}{BQ}=\frac{3}{4}$,点$E$恰好落在$CD$的中点处,求$BC$的长.

答案:
22.
(1)证明:
∵四边形ABCD是矩形,
∴AD//BC,
∴∠EPQ = ∠BQP,∠PQE = ∠BQP,
∴∠EPQ = ∠PQE,
∴PE = QE。
(2)解:设$AP = x$,则$PD = 3 - x$,
∴$PD = DQ = BQ = 3 - x$,
∴$CQ = x$。
∵$QC^{2}+DC^{2}=DQ^{2}$,
∴$x^{2}+2^{2}=(3 - x)^{2}$,解得$x = \frac{5}{6}$,即AP的长为$\frac{5}{6}$。
(3)解:延长QE交AD的延长线于点M。
∵AD//BC,
∴∠M = ∠CQE,∠EDM = ∠C。
∵E为CD的中点,
∴$CE = DE$,
∴△CQE≌△DME (AAS),
∴$QC = DM$,$QE = EM$。
设$AP = 3y$,$BQ = 4y$,由折叠的性质知$QE = 4y$,
∴$EM = 4y$,
∴$QM = 8y$。
由
(1)知$PM = QM = 8y$,
∴$AM = 11y$。
∵$AD = BC$,
∴$4y + CQ = 11y - CQ$,
∴$CQ = \frac{7}{2}y$。
∵$CQ^{2}+CE^{2}=QE^{2}$,
∴$(\frac{7}{2}y)^{2}+1^{2}=(4y)^{2}$,解得$y = \frac{2}{15}\sqrt{15}$。
∴$BC = 4y + \frac{7}{2}y = \frac{15}{2}y = \sqrt{15}$。

22.
(1)证明:
∵四边形ABCD是矩形,
∴AD//BC,
∴∠EPQ = ∠BQP,∠PQE = ∠BQP,
∴∠EPQ = ∠PQE,
∴PE = QE。
(2)解:设$AP = x$,则$PD = 3 - x$,
∴$PD = DQ = BQ = 3 - x$,
∴$CQ = x$。
∵$QC^{2}+DC^{2}=DQ^{2}$,
∴$x^{2}+2^{2}=(3 - x)^{2}$,解得$x = \frac{5}{6}$,即AP的长为$\frac{5}{6}$。
(3)解:延长QE交AD的延长线于点M。
∵AD//BC,
∴∠M = ∠CQE,∠EDM = ∠C。
∵E为CD的中点,
∴$CE = DE$,
∴△CQE≌△DME (AAS),
∴$QC = DM$,$QE = EM$。
设$AP = 3y$,$BQ = 4y$,由折叠的性质知$QE = 4y$,
∴$EM = 4y$,
∴$QM = 8y$。
由
(1)知$PM = QM = 8y$,
∴$AM = 11y$。
∵$AD = BC$,
∴$4y + CQ = 11y - CQ$,
∴$CQ = \frac{7}{2}y$。
∵$CQ^{2}+CE^{2}=QE^{2}$,
∴$(\frac{7}{2}y)^{2}+1^{2}=(4y)^{2}$,解得$y = \frac{2}{15}\sqrt{15}$。
∴$BC = 4y + \frac{7}{2}y = \frac{15}{2}y = \sqrt{15}$。

查看更多完整答案,请扫码查看


