《2025年1加1轻巧夺冠完美期末八年级数学上册北师大版辽宁专版》

23.(13分)(沈阳于洪期末)
在平面直角坐标系中，对于图形M给出如下定义：将图形M上的一点P(a，b)变为点Q(a-b，a+b)，称Q为点P的关联点.图形M上所有点按上述方法变化后得到的点组成的图形记为图形N，称N为图形M的关联图形.
(1)求点(1，-3)的关联点的坐标.
(2)点A在直线y=x+2上，点A的关联点B在直线y=-3x+5上，求点A的坐标.
(3)如图，若点E(a，b)在第一象限，且a＞b，点E的关联点为F，判断△EOF的形状并证明.
(4)已知t＞0，三点坐标为A(t，0)，B(t，t)，C(0，t).若四边形OABC与其关联图形重合部分的面积为2，直线y=mx+n(m≠0)经过点(4，5)，且与该关联图形有交点，请直

接

写

出

m的最小值.

答案：
23.解:
(1)1−(−3)=4，1+(−3)=−2，
∴点(1，−3)的关联点的坐标为(4，−2)。
(2)
∵点A在直线y=x+2上，
∴设点A的坐标为(a,a+2)，又
∵a−(a−2)=−2，a+a+2 =2a+2，
∴点A的关联点B的坐标为(−2，2a +2)，
∵点B在直线y=−3x+5上，
∴2a+2 =11，解得a=$\frac{9}{2}$，
∴a+2=$\frac{13}{2}$，
∴点A的坐标为($\frac{9}{2}$,$\frac{13}{2}$)。
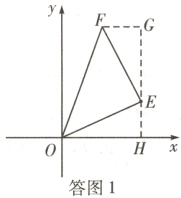
(3)△OEF为等腰直角三角形，证明如下：
∵a ＞b，
∴点E和点F在平面直角坐标系xOy中的位置如答图1所示，过点E作GH//y轴，交x 轴于点H，过点F作FG⊥HE的延长线于点G，则∠G=∠OHE=90°，
∵点E的坐标为(a,b)，
∴点F的坐标为(a−b,a+b)，OH=a，EH =b，FG=a−(a−b)=b，EG=a+b−b=a，
∴FG=EH，EG=OH，又
∵∠G=∠OHE，
∴△FGE≌△EHO(SAS)，
∴EF=OE，∠FEG =∠EOH，
∵∠EOH+∠OEH=90°，
∴∠FEG +∠OEH=90°，
∴∠OEF=90°，
∴△OEF为等腰直角三角形。

(4)
∵四点坐标为O(0,0)，A(t,0)，B(t,t)，C(0,t)，
∴点O关联点O'的坐标为(0,0)，点A关联点A'的坐标为(t,t)，点B关联点B'的坐标为(0，2t)，点C关联点C'的坐标为(−t，t)，如答图2，在平面直角坐标系xOy中画出图形，由图易知重叠部分为等腰直角三角形OCA'，
∴S△OCA'=$\frac{1}{2}$OC·CA'=$\frac{1}{2}$t²=2，解得t=2(负值舍去)，
∴三点坐标为A'(2，2)，B′(0,4)，C'(−2,2)，
∵直线y=mx+n经过点(4,5)，
∴y−5=m(x−4)，若直线与该关联图形有交点，则两个临界点为A'和B'，观察答图2易知当直线经过点B'时，倾斜程度最小，即m的值最小，将点B'的坐标(0，4)代入，得4−5=−4m，解得m=$\frac{1}{4}$，即m的最小值为$\frac{1}{4}$。