2025年1加1轻巧夺冠完美期末八年级数学上册北师大版辽宁专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年1加1轻巧夺冠完美期末八年级数学上册北师大版辽宁专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
21. (8 分)(沈阳沈河期末)
【问题情境】
某款电热水壶有两种工作模式: 煮沸模式和保温模式, 在煮沸模式下将水加热至 $100^{\circ}C$ 后自动进入保温模式, 此时电热水壶开始检测壶中水温. 若水温高于 $50^{\circ}C$, 水壶不加热; 若水温降至 $50^{\circ}C$ 水壶开始再加热, 水温达到 $100^{\circ}C$ 时停止加热……此后一直在保温模式下循环工作.
【实验探索】
数学小组对壶中水量 $a$(单位: L), 水温 $T$(单位: $^{\circ}C$)与加热时间 $t$(单位: 分钟)进行了观测和记录, 以下为该小组记录的部分数据.


对以上实验数据进行分析后, 该小组发现, 水壶中水量为 1 L 时, 无论在煮沸模式还是在保温模式下, 只要水壶开始加热, 壶中水温 $T$ 就是加热时间 $t$ 的一次函数.
(1)求表 1 中 $m$ 的值和表 2 中 $n$ 的值.
(2)根据表 2, 求出 1 L 水煮沸模式下 $T$ 关于 $t$ 的函数表达式, 并写出自变量 $t$ 的取值范围.
(3)根据表 2 中的数据, 完成以下内容:
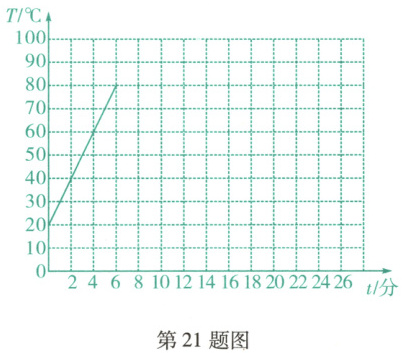
①在图中补全水温与时间(6 ~ 26 分钟)的函数图象;
②当 $t = 60$ 时, 求 $T$ 的值.
(4)假设温度降低过程中, 壶中水温与时间的函数关系和水量多少无关. 某天小明距离出门仅有 30 分钟, 他往水壶中注人 2.5 L 温度为 $20^{\circ}C$ 的水, 当水加热至 $100^{\circ}C$ 后立即关闭电源. 出门前, 他能否喝到低于 $50^{\circ}C$ 的水?
【问题情境】
某款电热水壶有两种工作模式: 煮沸模式和保温模式, 在煮沸模式下将水加热至 $100^{\circ}C$ 后自动进入保温模式, 此时电热水壶开始检测壶中水温. 若水温高于 $50^{\circ}C$, 水壶不加热; 若水温降至 $50^{\circ}C$ 水壶开始再加热, 水温达到 $100^{\circ}C$ 时停止加热……此后一直在保温模式下循环工作.
【实验探索】
数学小组对壶中水量 $a$(单位: L), 水温 $T$(单位: $^{\circ}C$)与加热时间 $t$(单位: 分钟)进行了观测和记录, 以下为该小组记录的部分数据.


对以上实验数据进行分析后, 该小组发现, 水壶中水量为 1 L 时, 无论在煮沸模式还是在保温模式下, 只要水壶开始加热, 壶中水温 $T$ 就是加热时间 $t$ 的一次函数.
(1)求表 1 中 $m$ 的值和表 2 中 $n$ 的值.
(2)根据表 2, 求出 1 L 水煮沸模式下 $T$ 关于 $t$ 的函数表达式, 并写出自变量 $t$ 的取值范围.
(3)根据表 2 中的数据, 完成以下内容:
①在图中补全水温与时间(6 ~ 26 分钟)的函数图象;
②当 $t = 60$ 时, 求 $T$ 的值.
(4)假设温度降低过程中, 壶中水温与时间的函数关系和水量多少无关. 某天小明距离出门仅有 30 分钟, 他往水壶中注人 2.5 L 温度为 $20^{\circ}C$ 的水, 当水加热至 $100^{\circ}C$ 后立即关闭电源. 出门前, 他能否喝到低于 $50^{\circ}C$ 的水?

答案:
21.解:
(1)由表1可知,水量每增加$0.5$ L,所需时间增加$3.5$分钟,
∴$m = 11.5 + 3.5 = 15$;由表2可知,在煮沸模式下,加热时间每增加$3$分钟,水温就上升$30^{\circ}C$,
∴在煮沸模式下,加热时间每增加$1$分钟,水温就上升$10^{\circ}C$,
∴$10(n - 6) = 100 - 80$,解得$n = 8$。
(2)在煮沸模式下,设$T$关于$t$的函数表达式为$T = kt + b$,把$t = 0$,$T = 20$和$t = 3$,$T = 50$代入表达式,得$\begin{cases} b = 20, \\ 3k + b = 50, \end{cases}$解得$\begin{cases} k = 10, \\ b = 20, \end{cases}$
∴$1$ L水煮沸模式下$T$关于$t$的函数表达式为$T = 10t + 20(0 \leq t \leq 8)$。
(3)①补全的水温与时间$(6 \sim 26$分钟$)$的函数图象如答图所示:

②当时间从26分开始,设时间为$t$时,水温加热到$100^{\circ}C$,在这个过程中每2分钟,水温升高$5^{\circ}C$,则每1分钟水温升高$5 ÷ 2 = 2.5(^{\circ}C)$,由此得$2.5(t - 26) = 100 - 60$,解得$t = 42$,$60 - 42 = 18$(分),根据表2的数据可知,$T = 100^{\circ}C$经过14分后降到了$T = 50^{\circ}C$,然后开始加热4分钟水温升到了$T = 60^{\circ}C$,
∴当$t = 60$时,$T = 60^{\circ}C$。
(4)由表1可知,$2.5$ L的水从$20^{\circ}C$加热到$100^{\circ}C$需要$18.5$分,$30 - 18.5 = 11.5$(分),由表2可知水温从$100^{\circ}C$降到$50^{\circ}C$需要$22 - m = 22 - 8 = 14$(分),
∵$11.5 + 14 = 22.5 < 30$,
∴出门前,他不能喝到低于$50^{\circ}C$的水。
21.解:
(1)由表1可知,水量每增加$0.5$ L,所需时间增加$3.5$分钟,
∴$m = 11.5 + 3.5 = 15$;由表2可知,在煮沸模式下,加热时间每增加$3$分钟,水温就上升$30^{\circ}C$,
∴在煮沸模式下,加热时间每增加$1$分钟,水温就上升$10^{\circ}C$,
∴$10(n - 6) = 100 - 80$,解得$n = 8$。
(2)在煮沸模式下,设$T$关于$t$的函数表达式为$T = kt + b$,把$t = 0$,$T = 20$和$t = 3$,$T = 50$代入表达式,得$\begin{cases} b = 20, \\ 3k + b = 50, \end{cases}$解得$\begin{cases} k = 10, \\ b = 20, \end{cases}$
∴$1$ L水煮沸模式下$T$关于$t$的函数表达式为$T = 10t + 20(0 \leq t \leq 8)$。
(3)①补全的水温与时间$(6 \sim 26$分钟$)$的函数图象如答图所示:

②当时间从26分开始,设时间为$t$时,水温加热到$100^{\circ}C$,在这个过程中每2分钟,水温升高$5^{\circ}C$,则每1分钟水温升高$5 ÷ 2 = 2.5(^{\circ}C)$,由此得$2.5(t - 26) = 100 - 60$,解得$t = 42$,$60 - 42 = 18$(分),根据表2的数据可知,$T = 100^{\circ}C$经过14分后降到了$T = 50^{\circ}C$,然后开始加热4分钟水温升到了$T = 60^{\circ}C$,
∴当$t = 60$时,$T = 60^{\circ}C$。
(4)由表1可知,$2.5$ L的水从$20^{\circ}C$加热到$100^{\circ}C$需要$18.5$分,$30 - 18.5 = 11.5$(分),由表2可知水温从$100^{\circ}C$降到$50^{\circ}C$需要$22 - m = 22 - 8 = 14$(分),
∵$11.5 + 14 = 22.5 < 30$,
∴出门前,他不能喝到低于$50^{\circ}C$的水。
查看更多完整答案,请扫码查看


