《2025年1加1轻巧夺冠完美期末八年级数学上册北师大版辽宁专版》

14. (沈阳沈河期末)在平面直角坐标系 $x O y$ 中, 一次函数 $y=k x$ 和 $y=-x+3$ 的图象如图所示, 则二元一次方程组 $\left\{\begin{array}{l}k x=y, \\ -x+3=y\end{array}\right.$ 的解为 ______ .

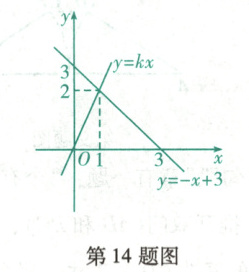
答案： $\begin{cases}x = 1, \\ y = 2\end{cases}$

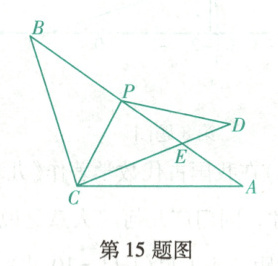
15. (沈阳皇姑期末)如图, 在 $\triangle A B C$ 中, $A C=B C=5 \mathrm{~cm}, A B=8 \mathrm{~cm}, P$ 是线段 $A B$ 上一动点, 将 $\triangle B C P$ 沿直线 $C P$ 折叠, 使点 $B$ 落在点 $D$ 处, $C D$ 交 $A P$ 于点 $E$. 当 $\triangle A C E$ 是直角三角形时, $B P$ 的长为$\frac{5}{2}$或1$\mathrm{cm}$.

答案：
$\frac{5}{2}$或1　[解析]分两种情况:①当∠AEC = 90°时，如答图1，
∵∠AEC = ∠DEP = 90°，设BP = xcm，
∵AC = BC = 5cm，CE⊥AB，
∴AE = BE = $\frac{1}{2}$AB = 4(cm)，
∴CE = $\sqrt{AC^2 - AE^2}=\sqrt{5^2 - 4^2}=3(cm)$，由折叠的性质知BC = CD = 5cm，BP = PD = xcm，
∴DE = CD - CE = 5 - 3 = 2(cm)，在Rt△DEP中，DE² + PE² = DP²，即4 + (4 - x)² = x²，解得x = $\frac{5}{2}$，
∴BP = $\frac{5}{2}$cm；②当∠ACE = 90°时，如答图2，过点C作CH⊥AB于点H，
∴∠AHC = ∠CHE = 90°，
∵AC = BC = 5cm，CH⊥AB，
∴∠B = ∠A，AH = BH = $\frac{1}{2}$AB = 4(cm)，
∴CH = $\sqrt{AC^2 - AH^2}=\sqrt{5^2 - 4^2}=3(cm)$，由折叠的性质知BC = CD = 5cm，∠BCP = ∠DCP，∠B = ∠D，
∴∠D = ∠A，
∵∠ECH + ∠HCA = 90°，∠HCA + ∠A = 90°，
∴∠ECH = ∠A，
∴∠ECH = ∠B，
∵∠CPH是△BCP的一个外角，
∴∠CPH = ∠B + ∠BCP，
∵∠PCH = ∠DCP + ∠ECH，
∴∠PCH = ∠CPH，
∴HC = HP = 3cm，
∴BP = BH - HP = 1(cm)，综上所述，BP的长为$\frac{5}{2}$cm或1cm.
　　 　　

16. (每小题 5 分, 共 10 分)(沈阳沈北期末)
计算: (1) $\sqrt{12} ÷ \sqrt{3}-\sqrt{\frac{1}{2}} × \sqrt{12}$; (2) $\sqrt{3}+(-2 \sqrt{3})^2-\left(\sqrt{48}-\sqrt{\frac{1}{2}} × \sqrt{6}\right)$.

答案： 16.解:
(1)原式 = 2 - $\sqrt{6}$.
(2)原式 = $\sqrt{3} + 12 - (4\sqrt{3} - \frac{1}{\sqrt{2}}×6)=\sqrt{3} + 12 - 4\sqrt{3} + \sqrt{3}=12 - 2\sqrt{3}$.