《2025年1加1轻巧夺冠完美期末八年级数学上册北师大版辽宁专版》

22. (12 分)(沈阳皇姑期末)
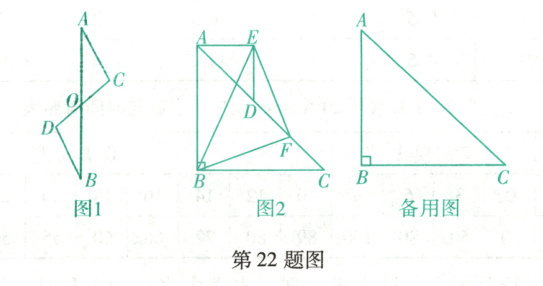
如图 1, $O$ 为线段 $AB,CD$ 的中点, 连接 $AC,BD$, 我们易得 $\triangle AOC\cong\triangle BOD$, 进而可以得到 $AC = BD$, 且 $AC// BD$.
如图 2, 在 $Rt\triangle ABC$ 中, $AB = CB,\angle ABC = 90^{\circ},D$ 为线段 $AC$ 上一点, 以 $AD$ 为斜边作等腰直角三角形 $AED$(点 $A,E,D$ 按顺时针顺序排列), 即 $AE = DE,\angle AED = 90^{\circ}$, 取 $CD$ 的中点 $F$, 连接 $BF,EF,BE$.
(1)求 $\angle EDF$ 的度数.
(2)求证: $\angle EBF = 45^{\circ}$.
(3)若将(2)中的 $D$ 改为直线 $AC$ 上一点, 其他条件不变, 设直线 $BE$ 与直线 $AC$ 相交于点 $G$, 当 $AB = CB = 6\sqrt{2},BF = 2\sqrt{10}$ 时, 求 $FG$ 的长.

答案：
22.
(1)解:
∵$AE = DE$，$\angle AED = 90^{\circ}$，
∴$\angle ADE = 45^{\circ}$，
∴$\angle EDF = 180^{\circ} - \angle ADE = 135^{\circ}$。
(2)证明:如答图1，延长$EF$至点$M$，使$FM = EF$，连接$CM$。由题干可知$DE = CM$，$EN // CM$，
∵$AE = DE$，$\angle AED = 90^{\circ}$，
∴$\angle EAD = 45^{\circ}$，$CM = AE$，
∵$AB = BC$，$\angle ABC = 90^{\circ}$，
∴$\angle BAC = 45^{\circ}$，
∴$\angle BAE = 90^{\circ}$，
∴$BA // DE$，
∴$BA // CM$，
∴$\angle BCM = \angle ABC = 90^{\circ}$，
∵$AB = BC$，
∴$\triangle ABE \cong \triangle CBM(SAS)$，
∴$BE = BM$，$\angle ABE = \angle CBM$，
∴$\angle EBM = \angle ABC = 90^{\circ}$，即$\triangle BEM$是等腰直角三角形，
∵$F$为$EM$的中点，
∴$\angle EBF = \frac{1}{2} \angle EBM = 45^{\circ}$。
(3)解:分两种情况:①当点$G$在线段$AC$上时，如答图1，在$BM$上截取$BH = BG$，连接$FH$，$CH$，由
(2)可知$\angle EBF = \angle FBH = 45^{\circ}$，又
∵$BF = BF$，
∴$\triangle GBF \cong \triangle HBF(SAS)$，
∴$FG = FH$，$BG = BH$，
∵$AB = BC$，$\angle ABG = \angle CBH$，
∴$\triangle ABG \cong \triangle CBH(SAS)$，
∴$\angle BAG = \angle BCH = 45^{\circ}$，$AG = CH$，
∴$\angle FCH = 45^{\circ} + 45^{\circ} = 90^{\circ}$，
∴$CF^{2} + CH^{2} = FH^{2}$，
∵$AB = CB = 6\sqrt{2}$，
∴$AC = \sqrt{2}AB = 12$，由
(2)知$\triangle BEF$为等腰直角三角形，
∵$BF = 2\sqrt{10}$，
∴$BE = \sqrt{2}BF = 4\sqrt{5}$，
∴$AE = \sqrt{BE^{2} - AB^{2}} = 2\sqrt{2}$，
∴$AD = \sqrt{2}AE = 4$，
∴$CD = AC - AD = 8$，
∵$F$为$CD$的中点，
∴$CF = 4$，设$FG = x$，则$AG = 8 - x$，
∵$CF^{2} + CH^{2} = FH^{2}$，
∴$4^{2} + (8 - x)^{2} = x^{2}$，解得$x = 5$，即$FG = 5$；②当点$G$在$CA$的延长线上时，如答图2，$CD = AC + AD = 12 + 4 = 16$，
∴$CF = 8$，$AF = 4$，由
(2)知$\angle EBF = 45^{\circ}$，同理可知$FG^{2} = AG^{2} + CF^{2}$，设$AG = x$，
∴$(12 + x - 8)^{2} = x^{2} + 8^{2}$，解得$x = 6$，即$AG = 6$，
∴$FG = 6 + 4 = 10$。
综上所述，$FG$的长为$5$或$10$。