《2025年1加1轻巧夺冠完美期末八年级数学上册北师大版辽宁专版》

23. (13 分)(丹东期末)
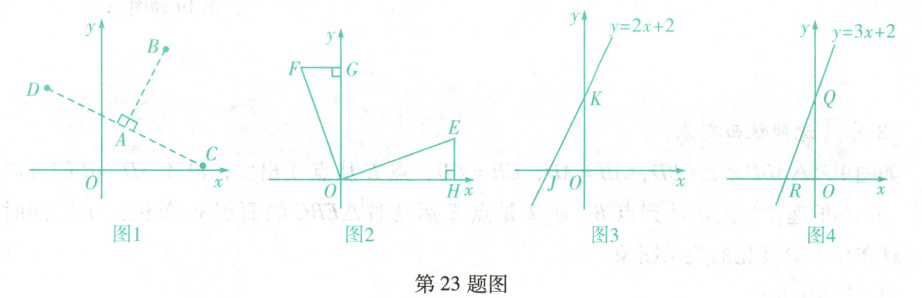
如图 1, 在平面直角坐标系 $x O y$ 中, $A, B$ 两点位置不同, 将点 $B$ 绕点 $A$ 按顺时针方向旋转 $90^{\circ}$ 后得到点 $C$, 称 $C$ 为点 $B$ 关于点 $A$ 的顺时针“垂链点”, 将点 $B$ 绕点 $A$ 按逆时针方向旋转 $90^{\circ}$ 后得到点 $D$, 称 $D$ 为点 $B$ 关于点 $A$ 的逆时针“垂链点”.
【问题初探】
(1)如图 2, 已知点 $O$ 的坐标为 $(0,0)$, 点 $E$ 的坐标为 $(3,1)$, 求出点 $E$ 关于点 $O$ 的“垂链点”的坐标. 小明提出连接 $O E$, 作 $O F \perp O E$, 使 $O F=O E, F$ 为点 $E$ 关于点 $O$ 的逆时针“垂链点”, 作 $F G \perp y$ 轴于点 $G$, 作 $E H \perp x$ 轴于点 $H$, 可以证明 $\triangle F G O \cong$ $\triangle E H O$, 则 $O H=O G=3, F G=E H=1$, 则点 $E$ 关于点 $O$ 的逆时针“垂链点” $F$ 的坐标为(-1，3), 点 $E$ 关于点 $O$ 的顺时针“垂链点”的坐标为(1，-3).
【方法迁移】
(2)如图 3, 已知直线 $y=2 x+2$ 与 $x$ 轴、 $y$ 轴分别交于 $J, K$ 两点, 求出点 $J$ 关于点 $K$ 的顺时针“垂链点”的坐标.
【拓展应用】
(3)如图 4, 已知直线 $y=3 x+2$ 与 $x$ 轴、 $y$ 轴分别交于 $R, Q$ 两点, 点 $P$ 在第二象限内,点 $P$ 的坐标为 $(-2, m)$. 若点 $Q$ 关于点 $P$ 的“垂链点”刚好落在直线 $y=3 x+2$ 上,请直

接

写

出

点 $Q$ 关于点 $P$ 的“垂链点”的坐标.
第 23 题图

答案： 23.解:
(1)(-1，3) (1，-3)【解析】由旋转的性质知∠EOF = 90°，OE = OF，
∵∠FOG + ∠GOE = 90°，∠HOE + ∠GOE = 90°，
∴∠FOG = ∠HOE，
∵FG⊥y轴于点G，EH⊥x轴于点H，
∴∠FGO = ∠EHO，在△FGO和△EHO中，
$\begin{cases}∠FGO = ∠EHO， \\ ∠FOG = ∠EOH， \\ OF = OE，\end{cases}$
∴△FGO≌△EHO(AAS)，
∴OH = OG = 3，FG = EH = 1，
∴点E关于点O的逆时针“垂链点”F的坐标为(-1，3)；当点E关于点O按顺时针方向旋转90°时，如答图1，同理可求FG = EH = 1，
∴点E关于点O的顺时针“垂链点”F的坐标为(1，-3).
(2)如答图2，
∵直线的表达式为y = 2x + 2，当x = 0时，y = 2，
∴OK = 2，当y = 0时，x = -1，
∴OJ = 1，同
(1)可证△ABK≌△KOJ，
∴AB = KO = 2，BK = OJ = 1，
∴OB = 3，
∴点J关于点K的顺时针“垂链点”A的坐标为(-2，3).
(3)
∵直线的表达式为y = 3x + 2，当x = 0时，y = 2，
∴OQ = 2，当y = 0时，x = $-\frac{2}{3}$，
∴OR = $\frac{2}{3}$，分两种情况:①当按顺时针方向旋转时，如答图3，点P的坐标为(-2，m)，点P所在的垂直于x轴的直线为l，过点C作CB⊥l于点B，过点Q作QA⊥l于点A，
∵点P的坐标为(-2，m)，
∴AQ = 2，AP = m - 2，同
(1)可证△PAQ≌△CBP，
∴BP = AQ = 2，BC = AP = m - 2，
∴BD = m + 2，
∴点C的坐标为(m - 4，m + 2)，
∵点Q关于点P的“垂链点”刚好落在直线y = 3x + 2上，
∴m + 2 = 3(m - 4) + 2，解得m = 6，
∴点C的坐标为(2，8)；②当按逆时针方向旋转时，如答图4，点P的坐标为(-2，m)，点P所在的垂直于x轴的直线为l，过点C作CB⊥l于点B，过点Q作QA⊥l于点A，
∵点P的坐标为(-2，m)，
∴AQ = 2，AP = 2 - m，同
(1)可证△PAQ≌△CBP，
∴BP = AQ = 2，BC = AP = 2 - m，
∴BD = 2 - m，
∴点C的坐标为(-m，m - 2)，
∵点Q关于点P的“垂链点”刚好落在直线y = 3x + 2上，
∴m - 2 = -3m + 2，
解得m = 1，
∴点C的坐标为(-1，-1).
综上所述，点Q关于点P的“垂链点”的坐标为(2，8)或(-1，-1).