2025年1加1轻巧夺冠完美期末八年级数学上册北师大版辽宁专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年1加1轻巧夺冠完美期末八年级数学上册北师大版辽宁专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
21. (8 分)
【阅读理解】
我们经常过某个点作已知直线的平行线, 以便利用平行线的性质来解决问题.
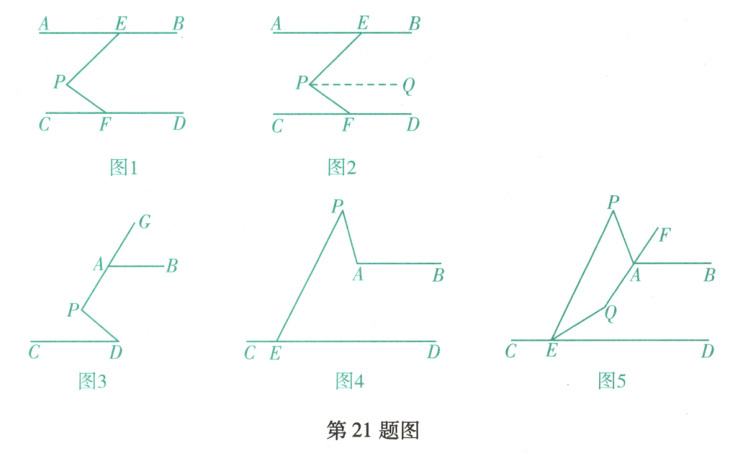
例如: 如图 1, 已知 $A B / / C D$, 点 $E, F$ 分别在直线 $A B, C D$ 上, 点 $P$ 在直线 $A B, C D$ 之间, 设 $\angle A E P=\alpha, \angle C F P=\beta$, 求证: $\angle P=\alpha+\beta$.
证明: 如图 2, 过点 $P$ 作 $P Q / / A B, \therefore \angle E P Q=\angle A E P=\alpha, \because P Q / / A B, A B / / C D$, $\therefore P Q / / C D, \therefore \angle F P Q=\angle C F P=\beta, \therefore \angle E P F=\angle E P Q+\angle F P Q=\alpha+\beta$, 即 $\angle E P F=\alpha$ $+\beta$.
【类比应用】
(1)如图 3, 已知 $A B / / C D, \angle D=15^{\circ}, \angle G A B=70^{\circ}$, 求 $\angle P$ 的度数.
(2)如图 4, 已知 $A B / / C D$, 点 $E$ 在直线 $C D$ 上, 点 $P$ 在直线 $A B$ 的上方, 连接 $P A, P E$,则 $\angle P A B, \angle C E P, \angle A P E$ 之间有何数量关系? 请说明理由.
【拓展应用】
(3)如图 5, 已知 $A B / / C D$, 点 $E$ 在直线 $C D$ 上, 点 $P$ 在直线 $A B$ 的上方, 连接 $P A, P E$, $\angle P E D$ 的平分线与 $\angle P A B$ 的平分线所在直线交于点 $Q$, 求 $2 \angle A Q E+\angle A P E$ 的值.
第 21 题图
【阅读理解】
我们经常过某个点作已知直线的平行线, 以便利用平行线的性质来解决问题.
例如: 如图 1, 已知 $A B / / C D$, 点 $E, F$ 分别在直线 $A B, C D$ 上, 点 $P$ 在直线 $A B, C D$ 之间, 设 $\angle A E P=\alpha, \angle C F P=\beta$, 求证: $\angle P=\alpha+\beta$.
证明: 如图 2, 过点 $P$ 作 $P Q / / A B, \therefore \angle E P Q=\angle A E P=\alpha, \because P Q / / A B, A B / / C D$, $\therefore P Q / / C D, \therefore \angle F P Q=\angle C F P=\beta, \therefore \angle E P F=\angle E P Q+\angle F P Q=\alpha+\beta$, 即 $\angle E P F=\alpha$ $+\beta$.
【类比应用】
(1)如图 3, 已知 $A B / / C D, \angle D=15^{\circ}, \angle G A B=70^{\circ}$, 求 $\angle P$ 的度数.
(2)如图 4, 已知 $A B / / C D$, 点 $E$ 在直线 $C D$ 上, 点 $P$ 在直线 $A B$ 的上方, 连接 $P A, P E$,则 $\angle P A B, \angle C E P, \angle A P E$ 之间有何数量关系? 请说明理由.
【拓展应用】
(3)如图 5, 已知 $A B / / C D$, 点 $E$ 在直线 $C D$ 上, 点 $P$ 在直线 $A B$ 的上方, 连接 $P A, P E$, $\angle P E D$ 的平分线与 $\angle P A B$ 的平分线所在直线交于点 $Q$, 求 $2 \angle A Q E+\angle A P E$ 的值.
第 21 题图

答案:
21.解:
(1)如答图1,延长BA至点H,
∵AB//CD,
∴∠P = ∠HAP + ∠D,
∵∠HAP = ∠GAB,∠GAB = 70°,
∴∠HAP = 70°,
∵∠D = 15°,
∴∠P = 85°.
(2)∠PAB + ∠CEP - ∠APE = 180°,理由如下:
如答图2,过点P作PM//AB,
∵AB//CD,
∴AB//CD//PM,
∴∠MPE = ∠CEP,∠MPA + ∠PAB = 180°,
∴∠MPE - ∠MPA - ∠PAB = ∠CEP - 180°,即∠APE - ∠PAB = ∠CEP - 180°,
∴∠PAB + ∠CEP - ∠APE = 180°.
(3)
∵AB//CD,
∴∠AQE = ∠BAQ + ∠DEQ,
∴2∠AQE = 2∠BAQ + 2∠DEQ = 2(180° - ∠BAF) + 2∠DEQ,又
∵QE,AF分别是∠PED与∠PAB的平分线,
∴2∠BAF = ∠PAB,2∠DEQ = ∠PED,
∴2∠AQE = 360° - ∠PAB + ∠PED,由
(2)知∠PAB + ∠CEP - ∠APE = 180°,
∴∠APE = ∠CEP + ∠PAB - 180°,
∴2∠AGE + ∠APE = 360° - ∠PAB + ∠PED + ∠CEP + ∠PAB - 180° = 180° + 180° = 360°,即2∠AGE + ∠APE = 360°.
(1)如答图1,延长BA至点H,
∵AB//CD,
∴∠P = ∠HAP + ∠D,
∵∠HAP = ∠GAB,∠GAB = 70°,
∴∠HAP = 70°,
∵∠D = 15°,
∴∠P = 85°.
(2)∠PAB + ∠CEP - ∠APE = 180°,理由如下:
如答图2,过点P作PM//AB,
∵AB//CD,
∴AB//CD//PM,
∴∠MPE = ∠CEP,∠MPA + ∠PAB = 180°,
∴∠MPE - ∠MPA - ∠PAB = ∠CEP - 180°,即∠APE - ∠PAB = ∠CEP - 180°,
∴∠PAB + ∠CEP - ∠APE = 180°.
(3)
∵AB//CD,
∴∠AQE = ∠BAQ + ∠DEQ,
∴2∠AQE = 2∠BAQ + 2∠DEQ = 2(180° - ∠BAF) + 2∠DEQ,又
∵QE,AF分别是∠PED与∠PAB的平分线,
∴2∠BAF = ∠PAB,2∠DEQ = ∠PED,
∴2∠AQE = 360° - ∠PAB + ∠PED,由
(2)知∠PAB + ∠CEP - ∠APE = 180°,
∴∠APE = ∠CEP + ∠PAB - 180°,
∴2∠AGE + ∠APE = 360° - ∠PAB + ∠PED + ∠CEP + ∠PAB - 180° = 180° + 180° = 360°,即2∠AGE + ∠APE = 360°.
查看更多完整答案,请扫码查看


