2025年1加1轻巧夺冠完美期末八年级数学上册北师大版辽宁专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年1加1轻巧夺冠完美期末八年级数学上册北师大版辽宁专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
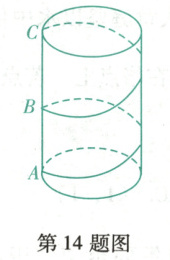
14. (辽阳期末)有一个圆柱体礼盒, 高 24 cm, 底面周长为 16 cm. 现准备在礼盒表面粘贴彩带作为装饰. 若彩带一端粘在 $A$ 处, 另一端绕礼盒侧面 2 周后粘贴在 $C$ 处 ($B$ 为 $AC$ 的中点), 则彩带的最短长度为
40
cm.
答案:
14.40 [解析]侧面展开后图形如答图,
∵高24cm,
∴AD = BC = 12cm,
∵底面周长为16cm,
∴BD = 16cm,在$Rt\triangle ABD$中,由勾股定理知$AB = \sqrt{AD^{2} + BD^{2}} = \sqrt{12^{2} + 16^{2}} = 20(cm)$,
∴彩带的最短长度为40cm。

14.40 [解析]侧面展开后图形如答图,
∵高24cm,
∴AD = BC = 12cm,
∵底面周长为16cm,
∴BD = 16cm,在$Rt\triangle ABD$中,由勾股定理知$AB = \sqrt{AD^{2} + BD^{2}} = \sqrt{12^{2} + 16^{2}} = 20(cm)$,
∴彩带的最短长度为40cm。

15. 如图, 在 $\triangle ABC$ 中, $\angle C = 90^{\circ},BC = 1,AC = 2\sqrt{2},P$ 是直线 $AB$ 上一点, 当 $\angle BPC = \frac{1}{2}\angle ABC$ 时, $\triangle BPC$ 的面积为
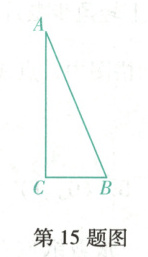
$\frac{\sqrt{2}}{3}$或$\frac{5\sqrt{2}}{9}$
.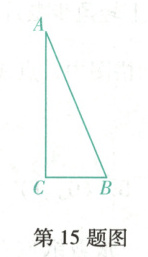
答案:
15.$\frac{\sqrt{2}}{3}$或$\frac{5\sqrt{2}}{9}$ [解析]
∵$\angle C = 90^{\circ}$,$BC = 1$,$AC = 2\sqrt{2}$,
∴$AB = \sqrt{AC^{2} + BC^{2}} = 3$。分两种情况:①当点$P$在$AB$的延长线上时,过点$C$作$CD \perp AB$于点$D$,如答图1,
∵$\angle BPC = \frac{1}{2} \angle ABC$,$\angle BPC + \angle BCP = \angle ABC$,
∴$\angle BPC = \angle BCP$,
∴$BC = BP = 1$,
∵$S_{\triangle ABC} = \frac{1}{2}AB · CD = \frac{1}{2}BC · AC$,即$\frac{1}{2} × 3 × CD = \frac{1}{2} × 1 × 2\sqrt{2}$,解得$CD = \frac{2\sqrt{2}}{3}$,
∴$S_{\triangle BPC} = \frac{1}{2}PB · CD = \frac{\sqrt{2}}{3}$;②当点$P$在线段$AB$上时,过点$C$作$CD \perp AB$于点$D$,延长$AB$到$Q$,使$BQ = BC = 1$,如答图2,
∵$BQ = BC$,
∴$\angle BQC = \angle BCQ$,
∴$\angle BQC = \frac{1}{2} \angle ABC$,
∴$\angle BPC = \frac{1}{2} \angle ABC$,
∴$\angle BPC = \angle BQC$,
∴$CP = CQ$,
∵$CD \perp AB$,
∴$PD = DQ$,由①知$CD = \frac{2\sqrt{2}}{3}$,
∴$BD = \sqrt{BC^{2} - CD^{2}} = \frac{1}{3}$,
∴$PB = PD + BD = DQ + BD = BQ + 2BD = \frac{5}{3}$,
∴$S_{\triangle BPC} = \frac{1}{2}PB · CD = \frac{1}{2} × \frac{5}{3} × \frac{2\sqrt{2}}{3} = \frac{5\sqrt{2}}{9}$。
综上所述,$\triangle BPC$的面积为$\frac{\sqrt{2}}{3}$或$\frac{5\sqrt{2}}{9}$。


15.$\frac{\sqrt{2}}{3}$或$\frac{5\sqrt{2}}{9}$ [解析]
∵$\angle C = 90^{\circ}$,$BC = 1$,$AC = 2\sqrt{2}$,
∴$AB = \sqrt{AC^{2} + BC^{2}} = 3$。分两种情况:①当点$P$在$AB$的延长线上时,过点$C$作$CD \perp AB$于点$D$,如答图1,
∵$\angle BPC = \frac{1}{2} \angle ABC$,$\angle BPC + \angle BCP = \angle ABC$,
∴$\angle BPC = \angle BCP$,
∴$BC = BP = 1$,
∵$S_{\triangle ABC} = \frac{1}{2}AB · CD = \frac{1}{2}BC · AC$,即$\frac{1}{2} × 3 × CD = \frac{1}{2} × 1 × 2\sqrt{2}$,解得$CD = \frac{2\sqrt{2}}{3}$,
∴$S_{\triangle BPC} = \frac{1}{2}PB · CD = \frac{\sqrt{2}}{3}$;②当点$P$在线段$AB$上时,过点$C$作$CD \perp AB$于点$D$,延长$AB$到$Q$,使$BQ = BC = 1$,如答图2,
∵$BQ = BC$,
∴$\angle BQC = \angle BCQ$,
∴$\angle BQC = \frac{1}{2} \angle ABC$,
∴$\angle BPC = \frac{1}{2} \angle ABC$,
∴$\angle BPC = \angle BQC$,
∴$CP = CQ$,
∵$CD \perp AB$,
∴$PD = DQ$,由①知$CD = \frac{2\sqrt{2}}{3}$,
∴$BD = \sqrt{BC^{2} - CD^{2}} = \frac{1}{3}$,
∴$PB = PD + BD = DQ + BD = BQ + 2BD = \frac{5}{3}$,
∴$S_{\triangle BPC} = \frac{1}{2}PB · CD = \frac{1}{2} × \frac{5}{3} × \frac{2\sqrt{2}}{3} = \frac{5\sqrt{2}}{9}$。
综上所述,$\triangle BPC$的面积为$\frac{\sqrt{2}}{3}$或$\frac{5\sqrt{2}}{9}$。


16. (每小题 5 分, 共 10 分)(辽阳期末)
(1)计算: $\sqrt[3]{-27}-(2 + \sqrt{3})^2 + 2×\sqrt{\frac{27}{4}}$;
(2)解方程组: $\begin{cases}4x - y = 30,\\x - 2y = -10.\end{cases}$
(1)计算: $\sqrt[3]{-27}-(2 + \sqrt{3})^2 + 2×\sqrt{\frac{27}{4}}$;
(2)解方程组: $\begin{cases}4x - y = 30,\\x - 2y = -10.\end{cases}$
答案:
16.解:
(1)原式$ = - 3 - (4 + 3 + 4\sqrt{3}) + 3\sqrt{3} = - 3 - 7 - 4\sqrt{3} + 3\sqrt{3} = - 10 - \sqrt{3}$。
(2)$\begin{cases}4x - y = 30 &①\\x - 2y = - 10&② \end{cases}$,$① × 2 - ②$,得$7x = 70$,解得$x = 10$,把$x = 10$代入$②$,得$10 - 2y = - 10$,解得$y = 10$,故此方程组的解为$\begin{cases} x = 10, \\ y = 10. \end{cases}$
(1)原式$ = - 3 - (4 + 3 + 4\sqrt{3}) + 3\sqrt{3} = - 3 - 7 - 4\sqrt{3} + 3\sqrt{3} = - 10 - \sqrt{3}$。
(2)$\begin{cases}4x - y = 30 &①\\x - 2y = - 10&② \end{cases}$,$① × 2 - ②$,得$7x = 70$,解得$x = 10$,把$x = 10$代入$②$,得$10 - 2y = - 10$,解得$y = 10$,故此方程组的解为$\begin{cases} x = 10, \\ y = 10. \end{cases}$
查看更多完整答案,请扫码查看


