《2025年1加1轻巧夺冠完美期末八年级数学上册北师大版辽宁专版》

22. （12分）（沈阳皇姑期末）
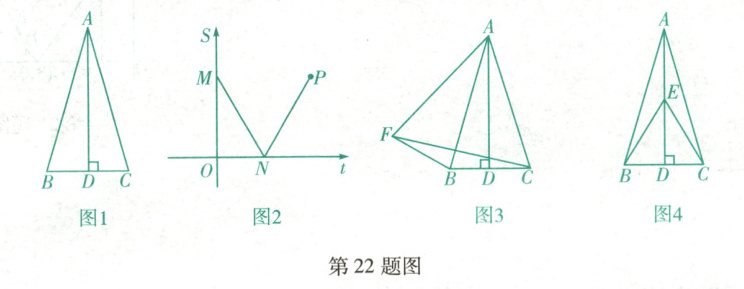
如图1，在$\triangle ABC$中，$AB = AC$，$AD \perp BC$于点$D$，在线段$AD$上，动点$E$以每秒$\sqrt{3}$个单位长度的速度从点$A$出发向终点$D$运动，连接$CE$，以$CE$为边作等边三角形$CEF$（点$C$，$E$，$F$按逆时针顺序排列），连接$BF$. 设点$E$的运动时间为$t$秒，$\triangle BCF$的面积为$S$，$S$与$t$的函数图象如图2所示（$S$，$t$均可为0），其中线段$MN$所在直线的表达式为$S = -\sqrt{3}t + 2\sqrt{3}$.
(1)当$t = 0$时，点$E$与点$A$重合，$\triangle CAF$为等边三角形，如图3，求$\triangle BCF$的面积$S$.
(2)当$EC = BC$时，连接$EB$，如图4.
①求此时$t$的值.
②求$BC$的长.
(3)在点$E$运动的过程中，若存在两个时刻$t_1$和$t_2$（$t_1 ＜ t_2$），对应的$\triangle BCF$的面积分别为$S_1$和$S_2$，当$t_2 - t_1 = 2$，且$S_1 = S_2$时，

请

直

接

写

出

$S_1$的值.

答案：
22.解：
(1)把t = 0代入$S = - \sqrt{3}t + 2\sqrt{3}$，解得$S = 2\sqrt{3}$。
(2)①
∵AB = AC，AD⊥BC于点D，
∴BD = CD，即AD垂直平分BC，
∴EB = EC。
∵EC = BC，
∴EB = EC = BC，
∴△EBC是等边三角形。此时点F运动到点B处，S = 0，
∴$- \sqrt{3}t + 2\sqrt{3} = 0$，解得t = 2。
②如答图1，
∵△CAF是等边三角形，
∴AC = CF，∠ACF = 60°，
∴∠ACF - ∠ECF = ∠BCE - ∠ECF，
∴∠BCF = ∠ACE。又
∵EC = BC，
∴△BCF≌△ACE(SAS)，
∴$S_{\triangle BCF} = S_{\triangle ACE} = \frac{1}{2}AE · CD = 2 × \sqrt{3}$，即$\frac{1}{2} × 2\sqrt{3}CD = 2\sqrt{3}$，解得CD = 2，
∴BC = 2CD = 4。 　　　
(3)如答图2，由
(2)知△BCF≌△ACE，
∴∠BFC = ∠CAD，
∴点F在过点B的定直线上运动。
∵$t_2 - t_1 = 2$，
∴$t_1 = 1$，$t_2 = 3$。当t = 1时，$S_1 = y = - \sqrt{3} × 1 + 2\sqrt{3} = \sqrt{3}$。