《2026年优选课堂必刷题高一数学全一册人教版》

6. 某地下车库在排气扇发生故障的情况下，测得空气中一氧化碳的含量达到了危险状态，经抢修后恢复正常。排气 $ 4 $ 分钟后测得车库内一氧化碳浓度为 $ 64 $ ppm（ppm 为浓度单位，$ 1 $ ppm 表示百万分之一），经检验知，该地下车库一氧化碳浓度 $ y $（单位：ppm）与排气时间 $ t $（单位：分钟）之间存在函数关系 $ y = 2^{7 - mt} $（$ m $ 为常数），则 $ m = $______；若空气中一氧化碳浓度不高于 $ 0.5 $ ppm 为正常，那么至少需要排气______分钟才能使这个地下车库中一氧化碳含量达到正常状态。

答案： 6.解析:$\because$函数$y = 2^{7 - mt}$（$m$为常数）经过点$(4,64)$，$\therefore 64 = 2^{7 - 4m}$，解得$m = \frac{1}{4}$.故$y = 2^{7 - \frac{1}{4}t}$.由$2^{7 - \frac{1}{4}t} \leq \frac{1}{2}$，解得$t \geq 32$.故至少排气32分钟，这个地下车库中的一氧化碳含量才能达到正常状态.
答案:$\frac{1}{4}$　32

7. 函数 $ f(x) = \ln x + x^3 - 9 $ 的零点所在的区间为（ ）

A.$ (0, 1) $
B.$ (1, 2) $
C.$ (2, 3) $
D.$ (3, 4) $

答案： 7.C　$f(1) = 1 - 9 = - 8 ＜ 0$，$f(2) = \ln 2 + 8 - 9 = \ln 2 - 1 ＜ 0$，$f(3) = \ln 3 + 27 - 9 = \ln 3 + 18 ＞ 0$，$\therefore f(2) · f(3) ＜ 0$，$\therefore$函数$f(x)$的零点所在的区间为$(2,3)$.故选C.

8. 用二分法求函数的零点，经过若干次运算后函数的零点在区间 $ (a, b) $ 内，当 $ |a - b| ＜ \varepsilon $（$ \varepsilon $ 为精确度）时，函数零点近似值 $ x_0 = \dfrac{a + b}{2} $ 与真实零点的误差最大不超过（ ）

A.$ \dfrac{\varepsilon}{4} $
B.$ \dfrac{\varepsilon}{2} $
C.$ \varepsilon $
D.$ 2\varepsilon $

答案： 8.B　真实零点离近似值$x_{0}$最远即靠近$a$或$b$，而$b - \frac{a + b}{2} = \frac{a + b}{2} - a = \frac{b - a}{2} = \frac{\epsilon}{2}$，因此误差最大不超过$\frac{\epsilon}{2}$.故选B.

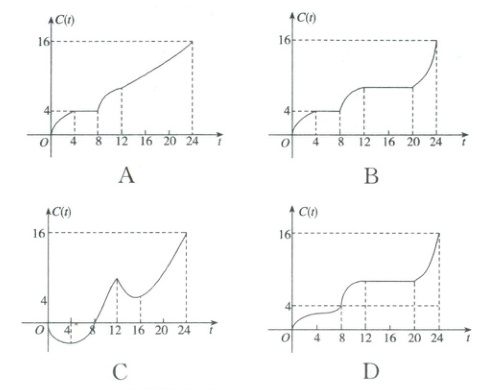
9. 老舍在《济南的冬天》中写到济南的冬天是没有风声的，济南的冬天是响晴的，济南真得算个宝地。济南市某一天内的气温 $ Q(t) $（单位：$ ° C $）与时刻 $ (t) $（单位：h）之间的关系如图所示，令 $ C(t) $ 表示时间段 $ [0, t] $ 内的温差（即时间段 $ [0, t] $ 内最高温度与最低温度的差），$ C(t) $ 与 $ t $ 之间的函数关系用下列图象表示，则下列正确的图象是（ ）

答案： 9.D　由题意$C(t)$，从0到4逐渐增大，从4到8不变，从8到12逐渐增大，从12到20不变，从20到24又逐渐增大，从4到8不变，是常数，该常数为2，只有D满足.故选D.

10. 有一组实验数据如下：

现准备用下列函数中的一个近似地表示这些数据满足的规律，其中最接近的一个是（ ）

A.$ V = \log_2 t $
B.$ V = \log_{\frac{1}{2}} t $
C.$ V = \dfrac{t^2 - 1}{2} $
D.$ V = 2t - 2 $

答案： 10.C　当$t = 4$时，选项A中的$V = \log_{2}4 = 2$，故A错误；选项B中的$V = \log_{\frac{1}{2}}4 = - 2$，故B错误；选项C中的$V = \frac{4^{2} - 1}{2} = 7.5$正确.故选C.

11. （多选题）某工厂生产一种溶液，按市场要求杂质含量不得超过 $ 0.1\% $，而这种溶液最初的杂质含量为 $ 2\% $，现进行过滤，已知每过滤一次杂质含量减少 $ \dfrac{1}{3} $，则使产品达到市场要求的过滤次数可以为（参考数据：$ \lg 2 \approx 0.301 $，$ \lg 3 \approx 0.477 $）（ ）

A.$ 6 $
B.$ 9 $
C.$ 8 $
D.$ 7 $

答案： 11.BC　设经过$n$次过滤，产品达到市场要求，则$\frac{2}{100} × (\frac{2}{3})^{n} \leq \frac{1}{1000}$，即$(\frac{2}{3})^{n} \leq \frac{1}{20}$，由$n\lg\frac{2}{3} \leq - \lg 20$，即$n(\lg 2 - \lg 3) \leq - (1 + \lg 2)$，得$n \geq \frac{1 + \lg 2}{\lg 3 - \lg 2} \approx 7.4$.故选BC.