《2026年优选课堂必刷题高一数学全一册人教版》

[例] (2025·广东深圳·高一统考质量检测) 已知函数 $ f(x) $ 是定义在 $ \mathbf{R} $ 上的奇函数, 且 $ f(x)=\frac{2 x}{x^{2}+a x+2} $.
(1) 求实数 $ a $ 的值;
(2) 对于 $ \forall x \in[1,2], m f(x)-3 \leqslant 0 $ 成立, 求实数 $ m $ 的取值范围.

答案： [解]
(1) $ \because f(x)=\frac{2 x}{x^{2}+a x+2} $ 是定义在 $ \mathbf{R} $ 上的奇函数, $ \because f(-x)=-f(x) $, $ \therefore \frac{-2 x}{x^{2}-a x+2}=-\frac{2 x}{x^{2}+a x+2} $, 于是, $ a x=0 $, $ x \in \mathbf{R} $, 因此 $ a=0 $;
(2) $ \because m f(x)-3 \leqslant 0 $ 在 $ x \in[1,2] $ 上恒成立, $ \therefore m \frac{2 x}{x^{2}+2} \leqslant 3 $ 在 $ x \in[1,2] $ 上成立, 于是, $ m \leqslant \frac{3}{2}\left(x+\frac{2}{x}\right) $ 在 $ x \in[1,2] $ 上恒成立, 记 $ g(x)=\frac{3}{2}\left(x+\frac{2}{x}\right) \geqslant \frac{3}{2} × 2 \sqrt{2}=3 \sqrt{2} $, 当且仅当 $ x=\frac{2}{x} $, 即 $ x=\sqrt{2} $ 等号成立. 因此, $ g(x)_{\min }=3 \sqrt{2} $, 即 $ m \leqslant 3 \sqrt{2} $, 所以, 实数 $ m $ 的取值范围为 $ (-\infty, 3 \sqrt{2}] $.

1. (2025·云南德宏·高一统考质量检测)下列函数既是幂函数又是奇函数的是（ ）

A.$ y = \sqrt[3]{x} $
B.$ y = \frac{1}{x^2} $
C.$ y = 2x^2 $
D.$ y = x + \frac{1}{x} $

答案： 1.A　对于A，由幂函数的定义知$y = \sqrt[3]{x} = x^{\frac{1}{3}}$是幂函数，由题意可知$f(x)$的定义域为$\mathbf{R}$，$f(-x) = \sqrt[3]{-x} = - \sqrt[3]{x} = -f(x)$，所以$f(x)$是奇函数，符合题意；故A正确；对于B，由幂函数的定义知$y = \frac{1}{x^{2}} = x^{-2}$是幂函数，由题意可知$f(x)$的定义域为$(-\infty,0)\cup(0,+\infty)$，$f(-x)=\frac{1}{(-x)^{2}}=\frac{1}{x^{2}}=f(x)$，所以$f(x)$是偶函数，不符合题意；故B错误；对于C，由幂函数的定义知$y = 2x^{2}$不是幂函数，不符合题意；故C错误；对于D，由幂函数的定义知$y = x + \frac{1}{x}$不是幂函数，不符合题意；故D错误.故选：A.

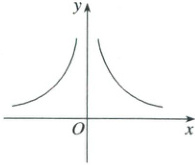
2. (2025·全国·对口高考)已知幂函数$ y = x^{\frac{p}{q}} $（$ p,q \in \mathbf{Z} $且$ p $与$ q $互质）的图象如图所示，则（ ）


A.$ p $、$ q $均为奇数且$ \frac{p}{q} ＜ 0 $
B.$ p $为奇数，$ q $为偶数且$ \frac{p}{q} ＜ 0 $
C.$ p $为奇数，$ q $为偶数且$ \frac{p}{q} ＞ 0 $
D.$ p $为偶数，$ q $为奇数且$ \frac{p}{q} ＜ 0 $

答案： 2.D　由图象知函数为偶函数，所以$p$为偶数，且由图象的形状判定$\frac{p}{q}＜0$，又因为$p$与$q$互质，所以$q$为奇数.故选：D.

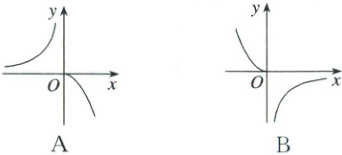
3. (2025·新疆阿勒泰·统考质量检测)已知函数则函数$ f(x) = \begin{cases} x^2, x \geq 0, \\ \frac{1}{x}, x ＜ 0, \end{cases} g(x) = f(-x) $，则函数$ g(x) $的图象大致是（ ）

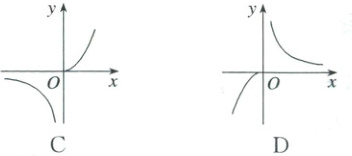
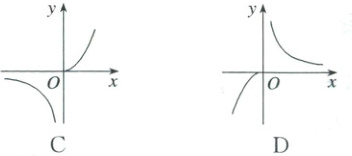
答案：
3.B　因为$g(x)=f(-x)$，所以$g(x)$图象与$f(x)$的图象关于$y$轴对称，由$f(x)$解析式，作出$f(x)$的图象如图
　　　　　　　　　
　从而可得$g(x)$图象为B选项.故选：B.