《2026年优选课堂必刷题高一数学全一册人教版》

[例] (1)$\sqrt[5]{(-2)^{5}}+(\sqrt[5]{-2})^{5}$；
(2)$\sqrt[6]{(-2)^{6}}+(\sqrt[6]{2})^{6}$；
(3)$\sqrt[4]{(x + 2)^{4}}$.

答案： [解]
(1)原式$=(-2)+(-2)=-4$.
(2)原式$=\vert -2\vert + 2 = 2 + 2 = 4$.
(3)原式$=\vert x + 2\vert =\begin{cases}x + 2,x\geqslant -2,\\ -x - 2,x ＜ -2.\end{cases}$

[例] 已知$-1 ＜ x ＜ 2$，化简$\sqrt{x^{2}-4x + 4}-\sqrt{x^{2}+2x + 1}$.

答案： [解] $\because -1 ＜ x ＜ 2$，$\therefore x - 2 ＜ 0$，$x + 1 ＞ 0$，
$\therefore\sqrt{x^{2}-4x + 4}-\sqrt{x^{2}+2x + 1}=\vert x - 2\vert -\vert x + 1\vert = 2 - x - (x + 1) = 1 - 2x$.

1. (2025·高一课时练习)函数①$y = 4^{x}$；②$y = x^{4}$；③$y = - 4^{x}$；④$y = ( - 4)^{x}$；⑤$y = \pi^{x}$；⑥$y = 4x^{2}$；⑦$y = x^{x}$；⑧$y = (a - 1)^{x}(a ＞ 1)$中，是指数函数的是______.

答案： 1.解析：因为指数函数为$y=a^{x}(a＞0$且$a\neq1)$，故①⑤正确；由幂函数定义知，$y=x^{a}$是幂函数，故②不正确；由指数函数的定义知，③④⑥⑦均不是指数函数；对于⑧，当$a=2$时，$y=(a-1)^{x}=1^{x}$，不是指数函数.故答案为：①⑤.
答案：①⑤

2. (2025·全国·高一假期作业)如果函数$f(x) = 2a·3^{x}$和$g(x) = 2^{x - (b + 3)}$都是指数函数，则$a^{b} =$（ ）

A.$\frac{1}{8}$
B.$1$
C.$9$
D.$8$

答案： 2.D 根据题意可得$2a=1\Leftrightarrow a=\frac{1}{2}$，$-(b+3)=0\Leftrightarrow b=-3$，则$a^{b}=(\frac{1}{2})^{-3}=8$.故选：D.

3. (多选题)(2025·全国·高一专题练习)已知函数$f(x) = a^{x + 1}+2(a ＞ 0$且$a\neq1)$的图象过定点$(a - 3,3)$，则（ ）

A.$a = 3$
B.$f(1) = 6$
C.$f(x)$为$\mathbf{R}$上的增函数
D.$f(x)＞10$的解集为$(2,+\infty)$

答案： 3.BCD 由题意可得$a^{a-2}+2=3$恒成立，故$a=2$，A错误；因为根据题意，得$a=2$，$\therefore f(x)=2^{x+1}+2$，所以$f(1)=2^{2}+2=6$，故B正确，$\because f(x)=2^{x+1}+2$，所以，$f(x)$为$\mathbf{R}$上的增函数，C正确；$f(x)=2^{x+1}+2＞10$，解得$x＞2$，D正确.故选：BCD.

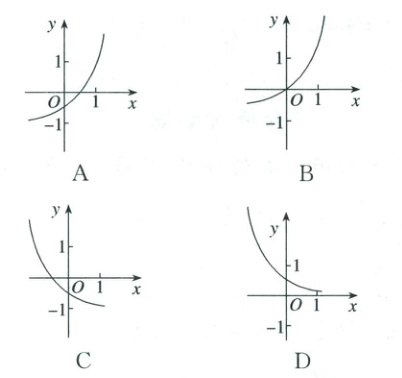
4. (2025·全国·高一假期作业)函数$f(x) = a^{x}-\frac{1}{a}(a ＞ 0,a\neq1)$的图象可能是（ ）

答案： 4.C 当$a＞1$时，$\frac{1}{a}\in(0,1)$，因此$0＜f(0)=1-\frac{1}{a}＜1$，且函数$f(x)=a^{x}-\frac{1}{a}$在$\mathbf{R}$上单调递增，故A、B均不符合；当$0＜a＜1$时，$\frac{1}{a}＞1$，因此$f(0)=1-\frac{1}{a}＜0$，且函数$f(x)=a^{x}-\frac{1}{a}$在$\mathbf{R}$上单调递减，故C符合，D不符合.故选：C.

5. (2025·全国·专题练习)已知$(\frac{1}{2})^{a}＜(\frac{1}{2})^{b}＜\frac{1}{2}$，则（ ）

A.$a^{a}＞a^{b}＞b^{b}$
B.$a^{a}＞b^{b}＞a^{b}$
C.$b^{b}＞a^{a}＞a^{b}$
D.$a^{b}＞b^{b}＞a^{a}$

答案： 5.A 因为函数$y=(\frac{1}{2})^{x}$在$\mathbf{R}$上单调递减，$(\frac{1}{2})^{a}＜(\frac{1}{2})^{b}$，所以$a＞b＞1$，因为函数$y=a^{x}(a＞1)$在$\mathbf{R}$为增函数，所以$a^{a}＞a^{b}$，又$y=x^{b}(b＞1)$在$(0,+\infty)$上单调递增，所以$a^{b}＞b^{b}$，综上，$a^{a}＞a^{b}＞b^{b}$.故选：A.