《2026年优选课堂必刷题高一数学全一册人教版》

1. 如图所示，这是某通讯公司规定的打某国际长途电话所需要付的电话费 $ y $（元）与通话时间 $ t $（分钟）之间的函数关系图象。根据图象填空：

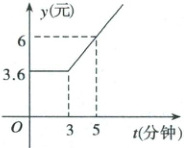
①通话 $ 2 $ 分钟，需要付电话费______元；
②通话 $ 5 $ 分钟，需要付电话费______元；
③如果 $ t \geqslant 3 $，则电话费 $ y $（元）与通话时间 $ t $（分钟）之间的函数关系式为______。

答案： 1.解析:①由图象可知，当$t \leq 3$时，电话费都是3.6元.
②由图象可知，当$t = 5$时，$y = 6$，需付电话费6元.
③易知当$t \geq 3$时，图象过点$(3,3.6)$，$(5,6)$，待定系数求得$y = 1.2t(t \geq 3)$.
答案:①3.6　②6　③$y = 1.2t(t \geq 3)$

2. 某品牌电动车有两个连锁店，其月利润（单位：元）分别为 $ y_1 = -5x^2 + 900x - 16000 $，$ y_2 = 300x - 2000 $，其中 $ x $ 为销售量。若某月两店共销售了 $ 110 $ 辆电动车，则最大利润为（ ）

A.$ 11000 $ 元
B.$ 22000 $ 元
C.$ 33000 $ 元
D.$ 40000 $ 元

答案： 2.C　设两个店分别销售出$x$与$110 - x$辆电动车，则两店月利润$L = - 5x^{2} + 900x - 16000 + 300(110 - x) - 2000 = - 5x^{2} + 600x + 15000 = - 5(x - 60)^{2} + 33000$，所以当$x = 60$时，两店的月利润取得最大值，为33000元.故选C.

3. 某商店进货单价为 $ 45 $ 元，若按 $ 50 $ 元一个销售，能卖出 $ 50 $ 个；若销售单价每涨 $ 1 $ 元，其销售量就减少 $ 2 $ 个，为了获得最大利润，此商品的最佳售价应为每个______元。

答案： 3.解析:设涨价$x$元，销售的利润为$y$元，则$y = (50 + x - 45)(50 - 2x) = - 2x^{2} + 40x + 250 = - 2(x - 10)^{2} + 450$，所以当$x = 10$，即销售价为60元时，$y$取得最大值.
答案:60

4. （2025·云南丽江·统考）华为消费者业务产品全面覆盖手机、移动宽带终端、终端云等，凭借自身的全球化网络优势、全球化运营能力，致力于将最新的科技带给消费者，让世界各地享受到技术进步的喜悦，以行践言，实现梦想。已知华为公司生产 mate 系列的某款手机的年固定成本为 $ 200 $ 万元，每生产 $ 1 $ 只还需另投入 $ 80 $ 元。设华为公司一年内共生产该款手机 $ x $ 万只并全部销售完，每万只的销售收入为 $ R(x) $ 万元，且 $ R(x) = \begin{cases} 2000 - 30x, & 0 ＜ x \leqslant 40 \\ \dfrac{37000}{x} - \dfrac{200000}{x^2}, & x ＞ 40 \end{cases} $
(1) 写出年利润 $ W $（万元）关于年产量 $ x $（万只）的函数解析式；
(2) 当年产量为多少万只时，华为公司在该款手机的生产中所获得的利润最大？并求出最大利润。

答案： 4.解:
(1)依题意，利用利润等于收入减去成本，可得:当$0 ＜ x \leq 40$时，$W(x) = xR(x) - (80x + 200) = x(2000 - 30x) - 80x - 200 = - 30x^{2} + 1920x - 200$；当$x ＞ 40$时，$W(x) = xR(x) - (80x + 200) = x(\frac{37000}{x} - \frac{200000}{x^{2}}) - 80x - 200 = - \frac{200000}{x} - 80x + 36800$；所以$W(x) = \begin{cases} - 30x^{2} + 1920x - 200,0 ＜ x \leq 40 \\ - \frac{200000}{x} - 80x + 36800,x ＞ 40 \end{cases}$
(2)当$0 ＜ x \leq 40$时，$W(x) = - 30x^{2} + 1920x - 200 = - 30(x - 32)^{2} + 30520$，所以当$x = 32$时，$W(x)_{\max} = 30520$；当$x ＞ 40$时，$W(x) = - \frac{200000}{x} - 80x + 36800 = - 80(\frac{2500}{x} + x) + 36800 \leq - 80 × 2\sqrt{\frac{2500}{x} · x} + 36800 = 28800$，当且仅当$\frac{2500}{x} = x$，即$x = 50$时，等号成立，此时$W(x)_{\max} = 28800$；因为$30520 ＞ 28800$，所以当年产量为32万只时，利润最大，最大利润为30520万元.

5. （2025·江苏南通·高一统考）已知销售甲、乙两种商品所得利润分别是 $ y_1 $（单位：万元）和 $ y_2 $（单位：万元），它们与投入资金 $ t $（单位：万元）的关系有经验公式分别为 $ y_1 = \dfrac{1}{5}\sqrt{t} $，$ y_2 = \dfrac{1}{5}at $，其中 $ a ＞ 0 $ 为常数。今将 $ 5 $ 万元资金经营甲、乙两种商品，设对甲种商品投入奖金 $ x $ 万元，其中 $ 1 \leqslant x \leqslant 4 $。
(1) 当 $ a = \dfrac{1}{3} $ 时，如何进行投资甲、乙两种商品才能使得总利润 $ y $ 最大；
(2) 存在 $ x \in [1, 4] $，使得甲、乙两种商品投资总利润等于 $ \dfrac{-4a + 3}{5} $，求 $ a $ 的取值范围。

答案： 5.解析:
(1)由题可知对甲种商品投入奖金$x$万元，则对乙种商品投入奖金$(5 - x)$万元，其中$1 \leq x \leq 4$，所以总利润$y = \frac{1}{5}\sqrt{x} + \frac{1}{15}(5 - x)$.令$t = \sqrt{x}$，则$1 \leq t \leq 2$，$x = t^{2}$，所以$y = \frac{1}{5}t + \frac{1}{15}(5 - t^{2}) = \frac{1}{15}(-t^{2} + 3t + 5)$，当$t = \frac{3}{2}$时，$y$取最大值，此时$x = \frac{9}{4}$，所以对甲种商品投入奖金$\frac{9}{4}$万元，对乙种商品投入奖金$\frac{11}{4}$万元时，总利润$y$最大.
(2)由题可知总利润$y = \frac{1}{5}\sqrt{x} + \frac{a}{5}(5 - x)$，令$t = \sqrt{x}$，则$1 \leq t \leq 2$，$x = t^{2}$，所以问题转化为存在$x \in [1,4]$，使得$y = \frac{1}{5}t + \frac{a}{5}(5 - t^{2}) = \frac{1}{5}[t + a(5 - t^{2})] = \frac{-4a + 3}{5}$有解，化简得$(t - 3) = a(t^{2} - 9)$，因为$1 \leq t \leq 2$，所以$t - 3 \neq 0$，从而$a = \frac{1}{t + 3}$，所以$\frac{1}{5} \leq a \leq \frac{1}{4}$.又由题知$a ＞ 0$，$\frac{-4a + 3}{5} ＞ 0$，所以$0 ＜ a ＜ \frac{3}{4}$，综上$\frac{1}{5} \leq a \leq \frac{1}{4}$.所以$a$的取值范围为$[\frac{1}{5},\frac{1}{4}]$.