《2025年同步练习册人民教育出版社八年级数学上册人教版山东专版》

2.利用因式分解计算:($\frac{35}{3}$)²−($\frac{5}{3}$)².

答案： 2. 解 原式$=(\frac{35}{3}+\frac{5}{3})×(\frac{35}{3}-\frac{5}{3})=\frac{40}{3}×10=\frac{400}{3}.$

利用因式分解简算:(1−$\frac{1}{22}$)×(1−$\frac{1}{32}$)×(1−$\frac{1}{42}$)×...×(1−$\frac{1}{3162}${×(1−$\frac{1}{3172}$).
 

答案： 解：原式=(1−$\frac{1}{2²}$)×(1−$\frac{1}{3²}$)×(1−$\frac{1}{4²}$)×...×(1−$\frac{1}{316²}$)×(1−$\frac{1}{317²}$)
=(1−$\frac{1}{2}$)(1+$\frac{1}{2}$)×(1−$\frac{1}{3}$)(1+$\frac{1}{3}$)×(1−$\frac{1}{4}$)(1+$\frac{1}{4}$)×...×(1−$\frac{1}{316}$)(1+$\frac{1}{316}$)×(1−$\frac{1}{317}$)(1+$\frac{1}{317}$)
=$\frac{1}{2}$×$\frac{3}{2}$×$\frac{2}{3}$×$\frac{4}{3}$×$\frac{3}{4}$×$\frac{5}{4}$×...×$\frac{315}{316}$×$\frac{317}{316}$×$\frac{316}{317}$×$\frac{318}{317}$
=$\frac{1}{2}$×$\frac{318}{317}$
=$\frac{159}{317}$

3.利用因式分解计算:
(1)[(2²−1)×(3²−1)×…×(2023²−1)×(2024²−1)]÷(1²×2²×3²2×…×2023²×2024²)=$\frac{2025}{4048}$;
(2)$\frac{1²−2}{2+4}$+$\frac{3²−42}{6+8}$+$\frac{52−62}{10+12}$+...十$\frac{1009²−10102}{2018+2020}$+$\frac{1011²−10122}{2022+2024}$=-253.

答案： $3. (1)\frac{2025}{4048} (2)-253$

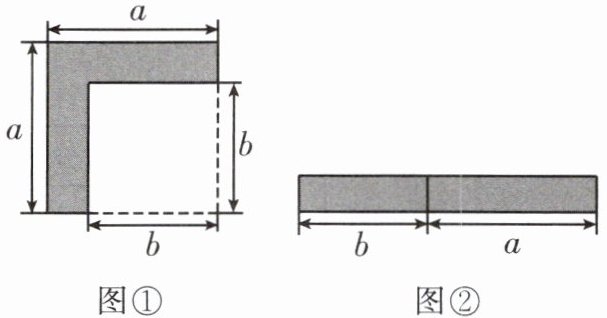
4.从边长为α的正方形中剪掉一个边长
为b的正方形(如图①)，然后将剩余部分拼成一个新的长方形(如图②).
(1)根据图①中阴影部分的面积与图
②中长方形的面积相等，可以验证的等式是
_;
(2)小明根据以上结论去计算(a+1).
(a²+1)(a≠1)时发现只需要在前面乘一个
$\frac{a−1}{a−1}$即可得到:$\frac{a−1}{a−1}$(a+1)(a²+1)=$\frac{a²−1}{a−1}$.
(a²+1)=$\frac{a−1}{a−1}$，请根据以上规律计算:当
a≠1时，(a+1)(a²+1)(a4+1).….
(a32+1)=$\frac{a^{64}-1}{a-1}$(直接写出结果即可);
(3)运用以上规律计算:(5+1)×(52+
1)×(54+1)×..×(564+1).

答案： 4. 解$（1）a^{2}-b^{2}=(a+b)(a-b)$
$（2）\frac{a^{64}-1}{a-1}$
（3）原式$=\frac{1}{4}×(5-1)×(5+1)×(5^{2}+1)×(5^{4}+1)×⋯×(5^{64}+1)=\frac{1}{4}×(5^{2}-1)×(5^{2}+1)×(5^{4}+1)×⋯×(5^{64}+1)=\frac{1}{4}×(5^{4}-1)×(5^{4}+1)×⋯×(5^{64}+1)=\frac{1}{4}×(5^{8}-1)×⋯×(5^{64}+1)⋯=\frac{1}{4}×(5^{64}-1)×(5^{64}+1)=\frac{5^{128}-1}{4}.$