第56页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
26. (6分) 现有两个电阻($R_1 > R_2$),一个电源(电压为$U$)、一个开关、导线若干。
(1) 根据条件总共能设计出______种不同电功率的电路,其中电功率最小的电路的电功率表达式为______。
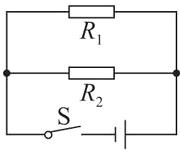
(2) 请在虚线框内设计出电功率最大的电路(要求画出完整的电路图)。

(1) 根据条件总共能设计出______种不同电功率的电路,其中电功率最小的电路的电功率表达式为______。
(2) 请在虚线框内设计出电功率最大的电路(要求画出完整的电路图)。

答案:
(1)4 $P=\frac {U^{2}}{R_{1}+R_{2}}$
(2)当两个电阻并联时,电路的总电阻最小,根据$P=\frac {U^{2}}{R}$可知,此时电路的电功率最大,故应将$R_{1}$和$R_{2}$并联接入电路,如图所示。
[解析]
(1)现有两个发热电阻($R_{1}>R_{2}$),其组合方式有4种,$R_{1}$和$R_{2}$单独接入电路,$R_{1}$和$R_{2}$串联接入电路,$R_{1}$和$R_{2}$并联接入电路;根据$P=\frac {U^{2}}{R}$可知,电路的总电阻不同,电路的电功率不同,故根据已知条件总共能设计出4种不同电功率的电路。当电路的总电阻最大时,根据$P=\frac {U^{2}}{R}$可知,电路的电功率最小;由题设条件可知,当$R_{1}$和$R_{2}$串联接入电路时总电阻最大,则电功率最小的电路的电功率表达式为$P=\frac {U^{2}}{R_{1}+R_{2}}$。
(1)4 $P=\frac {U^{2}}{R_{1}+R_{2}}$
(2)当两个电阻并联时,电路的总电阻最小,根据$P=\frac {U^{2}}{R}$可知,此时电路的电功率最大,故应将$R_{1}$和$R_{2}$并联接入电路,如图所示。

[解析]
(1)现有两个发热电阻($R_{1}>R_{2}$),其组合方式有4种,$R_{1}$和$R_{2}$单独接入电路,$R_{1}$和$R_{2}$串联接入电路,$R_{1}$和$R_{2}$并联接入电路;根据$P=\frac {U^{2}}{R}$可知,电路的总电阻不同,电路的电功率不同,故根据已知条件总共能设计出4种不同电功率的电路。当电路的总电阻最大时,根据$P=\frac {U^{2}}{R}$可知,电路的电功率最小;由题设条件可知,当$R_{1}$和$R_{2}$串联接入电路时总电阻最大,则电功率最小的电路的电功率表达式为$P=\frac {U^{2}}{R_{1}+R_{2}}$。
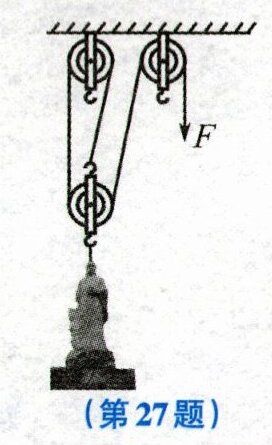
27. (6分) 陆羽公园矗立着由汉白玉制成的“茶圣”陆羽的雕像,其质量为$5.4t$。用如图所示的滑轮组将雕像匀速吊上$3m$的高台,已知提升雕像时,拉力$F的功率为6×10^3W$,绳子自由端的移动速度为$0.3m/s$。求:($g取10N/kg$)
(1) 滑轮组将雕像吊上$3m$高台需要的时间。
(2) 滑轮组对雕像做的有用功。
(3) 提升雕像的过程中滑轮组的机械效率。
(1) 滑轮组将雕像吊上$3m$高台需要的时间。
(2) 滑轮组对雕像做的有用功。
(3) 提升雕像的过程中滑轮组的机械效率。

答案:
(1)由题图可知,$n=3$,则绳子自由端移动的距离$s=3h=3×3m=9m$,根据$v=\frac {s}{t}$得所用的时间$t=\frac {s}{v}=\frac {9m}{0.3m/s}=30s$。
(2)雕像的重$G=mg=5.4×10^{3}kg×10N/kg=5.4×10^{4}N$,滑轮组对雕像做的有用功$W_{有用}=Gh=5.4×10^{4}N×3m=1.62×10^{5}J$。
(3)已知拉力F的功率为$6×10^{3}W,t=30s$,根据$P=\frac {W}{t}$得拉力做的总功$W_{总}=Pt=6×10^{3}W×30s=1.8×10^{5}J$,提升雕像的过程中滑轮组的机械效率$η=\frac {W_{有用}}{W_{总}}×100\% =\frac {1.62×10^{5}J}{1.8×10^{5}J}×100\% =90\% $。
(1)由题图可知,$n=3$,则绳子自由端移动的距离$s=3h=3×3m=9m$,根据$v=\frac {s}{t}$得所用的时间$t=\frac {s}{v}=\frac {9m}{0.3m/s}=30s$。
(2)雕像的重$G=mg=5.4×10^{3}kg×10N/kg=5.4×10^{4}N$,滑轮组对雕像做的有用功$W_{有用}=Gh=5.4×10^{4}N×3m=1.62×10^{5}J$。
(3)已知拉力F的功率为$6×10^{3}W,t=30s$,根据$P=\frac {W}{t}$得拉力做的总功$W_{总}=Pt=6×10^{3}W×30s=1.8×10^{5}J$,提升雕像的过程中滑轮组的机械效率$η=\frac {W_{有用}}{W_{总}}×100\% =\frac {1.62×10^{5}J}{1.8×10^{5}J}×100\% =90\% $。
28. (6分) 如图所示为一款无人驾驶汽车原型图。汽车自动驾驶时使用雷达传感器,以及激光测距器来了解周围的交通状况。该款车以$72km/h的速度在一段平直的公路上匀速行驶了8km$时,消耗汽油$1.5L$。假设燃油完全燃烧,发动机的效率为$30\%$,已知汽油的密度为$0.8×10^3kg/m^3$,汽油的热值为$4.5×10^7J/kg$。在这段运动过程中,求:
(1) 该汽车发动机做的有用功。
(2) 该汽车的输出功率。

(1) 该汽车发动机做的有用功。
(2) 该汽车的输出功率。

答案:
(1)由$ρ=\frac {m}{V}$得消耗汽油的质量$m=ρV=0.8×10^{3}kg/m^{3}×1.5×10^{-3}m^{3}=1.2kg$,汽油完全燃烧放出的热量$Q_{放}=mq=1.2kg×4.5×10^{7}J/kg=5.4×10^{7}J$;由$η=\frac {W}{Q_{放}}$得,汽油机的有用功$W=ηQ_{放}=30\% ×5.4×10^{7}J=1.62×10^{7}J$。
(2)由$v=\frac {s}{t}$得汽车运动的时间$t=\frac {s}{v}=\frac {8km}{72km/h}=\frac {1}{9}h=400s$,汽车的输出功率$P=\frac {W}{t}=\frac {1.62×10^{7}J}{400s}=4.05×10^{4}W$。
(1)由$ρ=\frac {m}{V}$得消耗汽油的质量$m=ρV=0.8×10^{3}kg/m^{3}×1.5×10^{-3}m^{3}=1.2kg$,汽油完全燃烧放出的热量$Q_{放}=mq=1.2kg×4.5×10^{7}J/kg=5.4×10^{7}J$;由$η=\frac {W}{Q_{放}}$得,汽油机的有用功$W=ηQ_{放}=30\% ×5.4×10^{7}J=1.62×10^{7}J$。
(2)由$v=\frac {s}{t}$得汽车运动的时间$t=\frac {s}{v}=\frac {8km}{72km/h}=\frac {1}{9}h=400s$,汽车的输出功率$P=\frac {W}{t}=\frac {1.62×10^{7}J}{400s}=4.05×10^{4}W$。
29. (6分) 太阳能热水器是吸收太阳辐射能给水加热的装置,具有环保、节能、使用寿命长、无污染等优点。某品牌太阳能热水器的储水质量为$200kg$。在该热水器装满水的情况下,经过一天$8h$的阳光照射,可以把水从$20℃加热到70℃$。
(1) 计算水吸收的热量。[$c_水 = 4.2×10^3J/(kg·℃)$]
(2)
(3) 若当天该热水器平均每平方米面积每小时接收的太阳能约为$3×10^6J$,该热水器的有效集热面积约为$2m^2$,则该热水器的能量转化效率为多少?
(1) 计算水吸收的热量。[$c_水 = 4.2×10^3J/(kg·℃)$]
(2)
0.525
如果用燃烧天然气的方式来加热这些水,水温也从$20℃上升至70℃$,不计热量损失,则需要完全燃烧______$m^3$的天然气。(天然气的热值为$8×10^7J/m^3$)(3) 若当天该热水器平均每平方米面积每小时接收的太阳能约为$3×10^6J$,该热水器的有效集热面积约为$2m^2$,则该热水器的能量转化效率为多少?
答案:
(1)水吸收的热量$Q_{吸}=c_{水}m_{水}(t-t_{0})=4.2×10^{3}J/(kg\cdot ^{\circ }C)×200kg×(70^{\circ }C-20^{\circ }C)=4.2×10^{7}J$。
(2)0.525
(3)太阳能热水器接收的太阳能$E=3×10^{6}J/(h\cdot m^{2})×8h×2m^{2}=4.8×10^{7}J$,则该热水器的能量转化效率$η=\frac {Q_{吸}}{E}×100\% =\frac {4.2×10^{7}J}{4.8×10^{7}J}×100\% =87.5\% $。
[解析]
(2)不计热量损失,天然气完全燃烧放出的热量$Q_{放}=Q_{吸}=4.2×10^{7}J$,由$Q_{放}=Vq$可得,需要完全燃烧天然气的体积$V=\frac {Q_{放}}{q}=\frac {4.2×10^{7}J}{8×10^{7}J/m^{3}}=0.525m^{3}$。
(1)水吸收的热量$Q_{吸}=c_{水}m_{水}(t-t_{0})=4.2×10^{3}J/(kg\cdot ^{\circ }C)×200kg×(70^{\circ }C-20^{\circ }C)=4.2×10^{7}J$。
(2)0.525
(3)太阳能热水器接收的太阳能$E=3×10^{6}J/(h\cdot m^{2})×8h×2m^{2}=4.8×10^{7}J$,则该热水器的能量转化效率$η=\frac {Q_{吸}}{E}×100\% =\frac {4.2×10^{7}J}{4.8×10^{7}J}×100\% =87.5\% $。
[解析]
(2)不计热量损失,天然气完全燃烧放出的热量$Q_{放}=Q_{吸}=4.2×10^{7}J$,由$Q_{放}=Vq$可得,需要完全燃烧天然气的体积$V=\frac {Q_{放}}{q}=\frac {4.2×10^{7}J}{8×10^{7}J/m^{3}}=0.525m^{3}$。
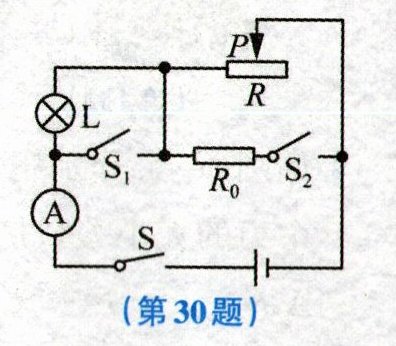
30. (8分) 在如图所示的电路中,电源电压为$6V$且保持不变,$R_0 = 30Ω$,滑动变阻器的规格为“$20Ω\ 1A$”,电流表的量程为“$0~0.6A$”,小灯泡上标有“$2.5V\ 1.25W$”字样,不考虑灯丝电阻变化,并保证长时间电路安全工作。计算:
(1) 当$S$闭合,$S_1$、$S_2$都断开,滑动变阻器的滑片移到最右端时,小灯泡在$1min$内消耗的电能。
(2) 当$S$闭合,$S_1$、$S_2$都断开时,电路消耗的最大功率。
(3) 当$S$、$S_1$、$S_2$都闭合时,滑动变阻器接入电路的最小阻值。
(1) 当$S$闭合,$S_1$、$S_2$都断开,滑动变阻器的滑片移到最右端时,小灯泡在$1min$内消耗的电能。
(2) 当$S$闭合,$S_1$、$S_2$都断开时,电路消耗的最大功率。
(3) 当$S$、$S_1$、$S_2$都闭合时,滑动变阻器接入电路的最小阻值。

答案:
(1)由$P=\frac {U^{2}}{R}$可得,小灯泡电阻$R_{L}=\frac {U_{L}^{2}}{P_{L}}=\frac {(2.5V)^{2}}{1.25W}=5\Omega $;由$P=UI$可得,小灯泡正常发光时的电流$I_{L}=\frac {P_{L}}{U_{L}}=\frac {1.25W}{2.5V}=0.5A$。当S闭合,$S_{1}$、$S_{2}$都断开,滑动变阻器的滑片移到最右端时,滑动变阻器的最大电阻与小灯泡L串联,则电路中的电流$I_{小}=\frac {U}{R_{滑大}+R_{L}}=\frac {6V}{20\Omega +5\Omega }=0.24A$;小灯泡在1min内消耗的电能$W=I_{小}^{2}R_{L}t=(0.24A)^{2}×5\Omega ×60s=17.28J$。
(2)当小灯泡正常发光时,电路中电流最大,$I_{最大}=I_{L}=0.5A$,则电路消耗的最大功率$P_{最大}=UI_{最大}=6V×0.5A=3W$。
(3)当S、$S_{1}$、$S_{2}$都闭合时,滑动变阻器与$R_{0}$并联,通过$R_{0}$的电流$I_{1}=\frac {U}{R_{0}}=\frac {6V}{30\Omega }=0.2A$;由电流表的量程可知,干路中的最大电流为0.6A,根据并联电路中干路电流等于各支路电流之和可得,通过滑动变阻器的最大电流$I_{滑最大}=I-I_{1}=0.6A-0.2A=0.4A$;根据欧姆定律可得,滑动变阻器接入电路的最小阻值$R_{滑最小}=\frac {U}{I_{滑最大}}=\frac {6V}{0.4A}=15\Omega $。
(1)由$P=\frac {U^{2}}{R}$可得,小灯泡电阻$R_{L}=\frac {U_{L}^{2}}{P_{L}}=\frac {(2.5V)^{2}}{1.25W}=5\Omega $;由$P=UI$可得,小灯泡正常发光时的电流$I_{L}=\frac {P_{L}}{U_{L}}=\frac {1.25W}{2.5V}=0.5A$。当S闭合,$S_{1}$、$S_{2}$都断开,滑动变阻器的滑片移到最右端时,滑动变阻器的最大电阻与小灯泡L串联,则电路中的电流$I_{小}=\frac {U}{R_{滑大}+R_{L}}=\frac {6V}{20\Omega +5\Omega }=0.24A$;小灯泡在1min内消耗的电能$W=I_{小}^{2}R_{L}t=(0.24A)^{2}×5\Omega ×60s=17.28J$。
(2)当小灯泡正常发光时,电路中电流最大,$I_{最大}=I_{L}=0.5A$,则电路消耗的最大功率$P_{最大}=UI_{最大}=6V×0.5A=3W$。
(3)当S、$S_{1}$、$S_{2}$都闭合时,滑动变阻器与$R_{0}$并联,通过$R_{0}$的电流$I_{1}=\frac {U}{R_{0}}=\frac {6V}{30\Omega }=0.2A$;由电流表的量程可知,干路中的最大电流为0.6A,根据并联电路中干路电流等于各支路电流之和可得,通过滑动变阻器的最大电流$I_{滑最大}=I-I_{1}=0.6A-0.2A=0.4A$;根据欧姆定律可得,滑动变阻器接入电路的最小阻值$R_{滑最小}=\frac {U}{I_{滑最大}}=\frac {6V}{0.4A}=15\Omega $。
查看更多完整答案,请扫码查看


