《2025年全优单元同步测试卷九年级科学全一册浙教版》

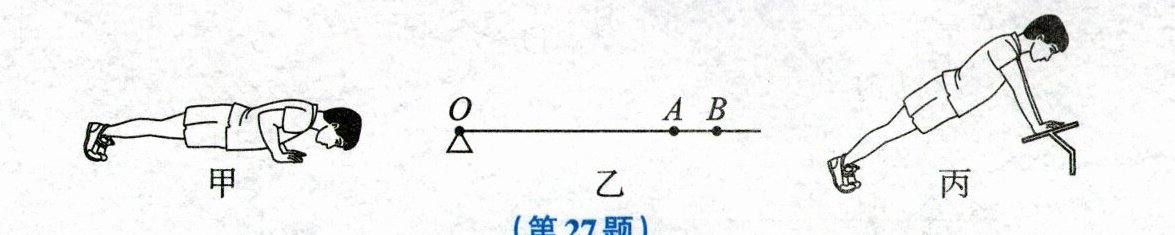
27. (7分)俯卧撑是一种常见的运动项目,采用不同的方式做俯卧撑,健身效果通常不同。如图甲所示为小明在水平地面上做俯卧撑保持静止时的情景,他的身体与地面平行,可抽象成如图乙所示的杠杆模型,地面对脚的力作用在O点,对手的力作用在B点,小明的重心在A点。已知小明受到的重力为600N,OA的长为1m,AB的长为0.2m。
(1)此类杠杆属于______(填“省力”或“费力”)杠杆。
(2)图乙中,地面对手的力$F_{1}$与身体垂直,则$F_{1}$为多少牛?
(3)图丙是小明手扶支架做俯卧撑保持静止时的情境,此时他的身体姿态与图甲相同,只是身体与水平地面成一定角度,支架对手的力$F_{2}$与他的身体垂直,且仍作用在B点,则$F_{1}$______(填“＞”“=”或“＜”)$F_{2}$。

答案：

(1)省力
(2)如图所示,O为支点，重力的力臂为$l_{A}$，$F_{1}$的力臂为$l_{B}$，由杠杆的平衡条件可得$F_{1}l_{B}=Gl_{A}$，则$F_{1}=\frac{Gl_{A}}{l_{B}}=\frac{600N×1m}{1m + 0.2m}=500N$。
　　　　　　
(3)＞

28. (6分)一名工人要将质量为100kg的木箱搬到1.5m高的车厢里,他将一块5m长的长板放在地面与车厢之间构成斜面,然后站在车上用400N的拉力在10s内将物体从斜面底端匀速拉到车厢里,如图所示。求:(g取10N/kg)
(1)工人所做的有用功。
(2)工人做功的功率。
(3)斜面的机械效率。

答案：
(1)木箱的重力$G =mg =100kg×10N/kg =1000N$，工人所做的有用功$W_{有用}=Gh =1000N×1.5m =1500J$。
(2)工人做的总功$W_{总}=Fs =400N×5m =2000J$，工人做功的功率$P_{总}=\frac{W_{总}}{t}=\frac{2000J}{10s}=200W$。
(3)斜面的机械效率$\eta=\frac{W_{有用}}{W_{总}}×100\%=\frac{1500J}{2000J}×100\% =75\%$。

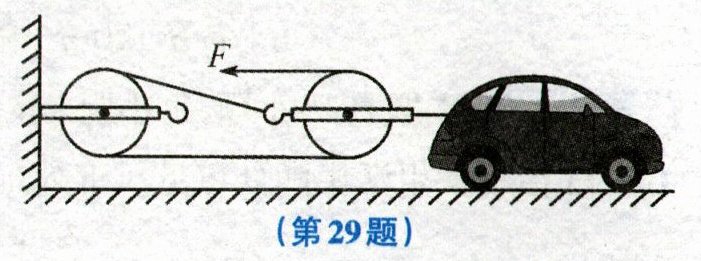
29. (6分)在一次车辆故障处置过程中,拖车所用装置的简化图如图所示。为了尽快疏通道路,交警只用了30s的时间,指挥拖车在水平路面上将质量为1.5t的故障车匀速拖离了现场。若故障车被拖离的速度是6m/s,绳子自由端的拉力F是500N,该装置的机械效率是80%,求:
(1)故障车在30s内通过的路程。
(2)拉力F在30s内所做的功。
(3)故障车在被拖离过程中受到的阻力。

答案：
(1)由$v=\frac{s}{t}$得故障车在30s内通过的路程$s_{车}=vt =6m/s×30s =180m$。
(2)由题图可知,$n =3$，绳子自由端移动的距离$s_{绳}=3s_{车}=3×180m =540m$，拉力F在30s内所做的功$W =Fs_{绳}=500N×540m =2.7×10^{5}J$。
(3)由题图可知,$n =3$，水平滑轮组的机械效率$\eta=\frac{W_{有用}}{W_{总}}×100\%=\frac{fs_{车}}{Fs_{绳}}×100\%=\frac{fs_{车}}{F×3s_{车}}×100\%=\frac{f}{3F}×100\%$，所以故障车在被拖离过程中受到的阻力$f =3F\eta =3×500N×80\% =1200N$。

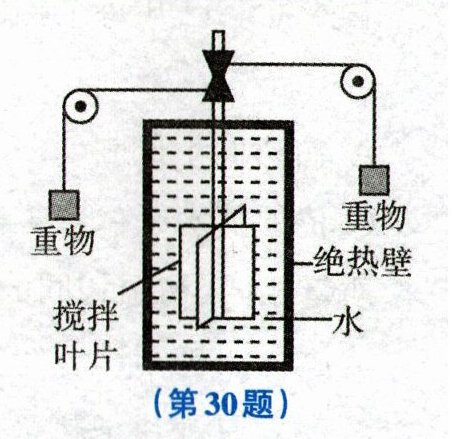
30. (8分)1845年,焦耳做了利用摩擦加热液体的实验。如图所示,他在容器里装入一定质量的水,中间安上带有叶轮的转轴,转轴上绕上绳子,绳子另一端通过滑轮与重物相连。当重物下降时,绳子拉动转轴转动,带动叶片旋转,由于叶片和水之间的摩擦,容器里的水的温度升高。通过测量和计算,可以比较重物减少的机械能与水增加的内能的关系。该实验为能量守恒定律的确立奠定了定量的实验基础。
(1)若实验中两个重物的总质量为25kg,下降高度为10m,则这两个重物减少的总机械能为2500J。
(2)若容器中水的质量为0.5kg,实验测得水温升高1℃,请计算水的内能的增加量。[$c_{水}= 4.2×10^{3}J/(kg·℃)$]
水的内能的增加量$Q =cm\Delta t =4.2×10^{3}J/(kg\cdot^{\circ}C)×0.5kg×1^{\circ}C =2100J$。
(3)某兴趣小组的同学多次重复以上实验,发现实验结果和能量守恒定律并不吻合。请写出造成这种结果的可能原因:转轴处存在摩擦(或液体散热)(写一种即可)。

答案：
(1)2500
(2)水的内能的增加量$Q =cm\Delta t =4.2×10^{3}J/(kg\cdot^{\circ}C)×0.5kg×1^{\circ}C =2100J$。
(3)转轴处存在摩擦(或液体散热)