9. 如图,函数 $ y = ax^{2} - 2x + 1 $ 和 $ y = ax - a $($ a $ 是常数,且 $ a \neq 0 $)在同一平面直角坐标系的图象可能是(

A.
B.
C.
D.
B
)
A.
B.
C.
D.
答案:
B
10. 如图,抛物线 $ y = ax^{2} + bx + c $($ a \neq 0 $),其顶点坐标为 $ (1, n) $,且与 $ x $ 轴的一个交点在 $ (3, 0) $ 和 $ (4, 0) $ 之间,下列结论不正确的是(
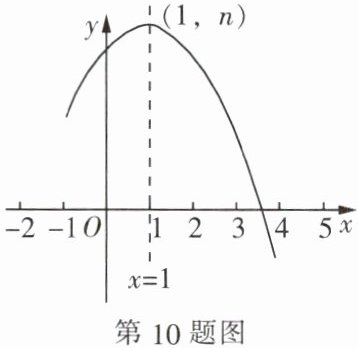
A.$ abc < 0 $
B.$ 2a + b = 0 $
C.$ 4a - 2b + c > 0 $
D.关于 $ x $ 的方程 $ ax^{2} + bx + c = 0 $($ a \neq 0 $)的另一个根在 -2 和 -1 之间
C
)
A.$ abc < 0 $
B.$ 2a + b = 0 $
C.$ 4a - 2b + c > 0 $
D.关于 $ x $ 的方程 $ ax^{2} + bx + c = 0 $($ a \neq 0 $)的另一个根在 -2 和 -1 之间
答案:
C
11. 抛物线 $ y = 2x^{2} + 4x - 1 $ 的顶点坐标是
$(-1,-3)$
.
答案:
$(-1,-3)$
12. 在平面直角坐标系 $ xOy $ 中,抛物线 $ y = x^{2} - 4x + 5 $ 与 $ y $ 轴交于点 $ C $,则点 $ C $ 的坐标为
$(0,5)$
.
答案:
$(0,5)$
13. 老师给出一个二次函数,甲、乙、丙三名同学各指出这个函数的一个性质.
甲:函数图象的顶点在 $ x $ 轴上;
乙:当 $ x < 1 $ 时,$ y $ 随 $ x $ 的增大而减小;
丙:该函数的形状与函数 $ y = x^{2} $ 的图象相同.
已知这三位同学的描述都正确,请你写出满足上述所有性质的一个二次函数表达式为
甲:函数图象的顶点在 $ x $ 轴上;
乙:当 $ x < 1 $ 时,$ y $ 随 $ x $ 的增大而减小;
丙:该函数的形状与函数 $ y = x^{2} $ 的图象相同.
已知这三位同学的描述都正确,请你写出满足上述所有性质的一个二次函数表达式为
$y=(x - 1)^{2}$(答案不唯一)
.
答案:
$y=(x - 1)^{2}$(答案不唯一)
14. 如图,抛物线 $ y = 2x^{2} - 8x + 6 $ 与 $ x $ 轴分别交于 $ A $,$ B $ 两点(点 $ A $ 在点 $ B $ 的左侧),与 $ y $ 轴交于点 $ C $,在其对称轴上有一动点 $ M $,连接 $ MA $,$ MC $,$ AC $,则当 $ \triangle MAC $ 的周长最小时,点 $ M $ 的坐标是
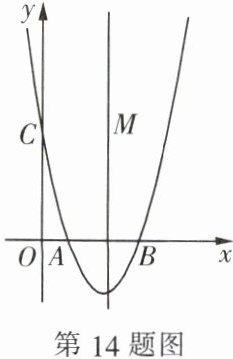
$(2,2)$
.
答案:
$(2,2)$
15. 已知飞机着陆后滑行的距离 $ y $(单位:m)关于滑行时间 $ t $(单位:s)的函数解析式是 $ y = 60t - \frac{3}{2}t^{2} $.在飞机着陆滑行中,最后3s滑行的距离是
13.5
m.
答案:
13.5
查看更多完整答案,请扫码查看


