《2025年新课程能力培养九年级数学上册人教版》

19. (8 分) 如图,AB 是⊙O 的直径,弦 CD⊥AB,E 是 CA 延长线上的一点,连接 DE 交⊙O 于点 F,连接 AF,CF.
(1) 若∠BAC = 20°,求∠AFC 的度数.
(2) 求证：∠AFC = ∠AFE.

答案：
(1) 连接AD，
∵AB是⊙O的直径，CD⊥AB，
∴AB垂直平分CD，
∴AC=AD，∠CAB=∠DAB=20°，
∴∠CAD=∠CAB+∠DAB=40°，
在△ACD中，AC=AD，
∴∠ACD=∠ADC，
∵∠ACD+∠ADC+∠CAD=180°，
∴2∠ADC=180°-40°=140°，∠ADC=70°，
∵∠AFC与∠ADC都是弧AC所对的圆周角，
∴∠AFC=∠ADC=70°．
(2) 证明：
∵∠AFE是△AFC的外角，
∴∠AFE=∠FCA+∠CAF，
∵∠FCA和∠FDA都是弧FA所对的圆周角，
∴∠FCA=∠FDA，
∵∠CAF和∠CDF都是弧CF所对的圆周角，
∴∠CAF=∠CDF，
∴∠AFE=∠FDA+∠CDF=∠CDA，
∵∠AFC与∠CDA都是弧AC所对的圆周角，
∴∠AFC=∠CDA，
∴∠AFC=∠AFE．

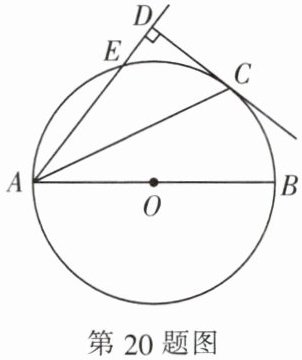
20. (8 分) 如图,AB 是⊙O 的直径,C 为⊙O 上一点,AD 和过点 C 的切线互相垂直,垂足为 D,AD 交⊙O 于点 E,AE = 3,CD = 2.
(1) 求证：AC 平分∠DAB.
(2) 求⊙O 的半径.

答案：
(1) 见解析；
(2) 5/2。

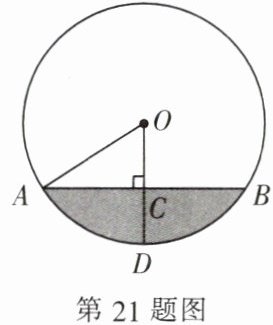
21. (8 分) 如图,水平放置的圆柱形排水管道的截面所在圆的半径 OA = 1 m,AB 表示水面的位置. 过点 O 作 OD⊥AB,垂足为 C,交⊙O 于点 D,水面高 CD = 0.5 m. 求截面上有水部分的面积.

答案：
∵OA=1m，OD⊥AB于C，
∴OD=OA=1m，AC=BC。
∵CD=0.5m，
∴OC=OD-CD=1-0.5=0.5m。
在Rt△OAC中，OA=1m，OC=0.5m，
∴AC=√(OA²-OC²)=√(1²-0.5²)=√(3/4)=√3/2 m，
∴AB=2AC=√3 m。
cos∠AOC=OC/OA=0.5/1=0.5，
∴∠AOC=60°，
∴∠AOB=2∠AOC=120°。
S扇形OAB=120°/360°×π×1²=π/3 m²。
S△OAB=1/2×AB×OC=1/2×√3×0.5=√3/4 m²。
有水部分面积=S扇形OAB - S△OAB=π/3 - √3/4。
答：截面上有水部分的面积为(π/3 - √3/4)m²。