16. (10 分) 一个不透明的口袋中放有只有颜色不同的 10 个球,其中有 5 个白球、3 个黑球、2 个红球,以下事件哪些是随机事件?哪些是必然事件?哪些是不可能事件?
(1) 从口袋中任取 1 个球是黑球.
(2) 从口袋中任取 5 个球,全是白球.
(3) 从口袋中任取 6 个球,没有白球.
(4) 从口袋中任取 9 个球,白、黑、红三种颜色的球都有.
(5) 从口袋中任取 1 个球,该球是黄色的.
(1) 从口袋中任取 1 个球是黑球.
(2) 从口袋中任取 5 个球,全是白球.
(3) 从口袋中任取 6 个球,没有白球.
(4) 从口袋中任取 9 个球,白、黑、红三种颜色的球都有.
(5) 从口袋中任取 1 个球,该球是黄色的.
答案:
(1) 随机事件。
(2) 随机事件。
(3) 不可能事件:因为口袋中只有$5$个非白球($3$个黑球和$2$个红球),所以无法取出$6$个非白球。
(4) 必然事件:因为口袋中总共有$10$个球,且三种颜色的球都有,所以取出$9$个球时,必然包含三种颜色的球。
(5) 不可能事件:因为口袋中没有黄色球。
(1) 随机事件。
(2) 随机事件。
(3) 不可能事件:因为口袋中只有$5$个非白球($3$个黑球和$2$个红球),所以无法取出$6$个非白球。
(4) 必然事件:因为口袋中总共有$10$个球,且三种颜色的球都有,所以取出$9$个球时,必然包含三种颜色的球。
(5) 不可能事件:因为口袋中没有黄色球。
17. (8 分) 已知电流在一定时间段内正常通过电子元件的概率是$\frac{1}{2}$. (提示:在一次实验中,每个电子元件的状态有两种可能:通电、断开,并且这两种状态的可能性相等)
(1) 如图 1,在一定时间段内,$A$,$B$之间电流能够正常通过的概率为
(2) 如图 2,求在一定时间段内,$C$,$D$之间电流能够正常通过的概率.
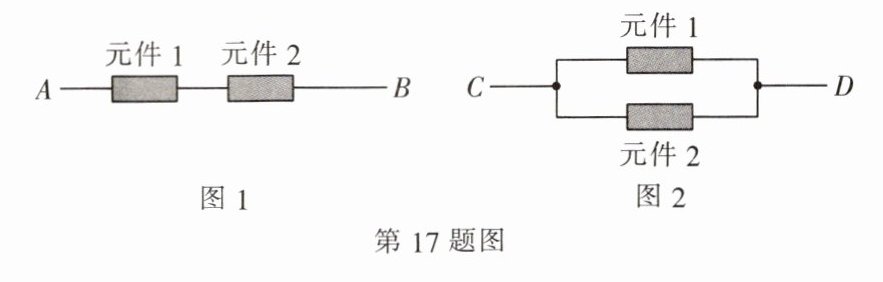
(1) 如图 1,在一定时间段内,$A$,$B$之间电流能够正常通过的概率为
$\frac{1}{4}$
.(2) 如图 2,求在一定时间段内,$C$,$D$之间电流能够正常通过的概率.

答案:
(1) $\frac{1}{4}$
(2) 列表如下:
| 元件1 | 元件2 |
| --- | --- |
| 通 | 通 |
| 通 | 断 |
| 断 | 通 |
| 断 | 断 |
共有4种等可能结果,其中至少一个元件通电的结果有3种,
$\therefore P=\frac{3}{4}$
(1) $\frac{1}{4}$
(2) 列表如下:
| 元件1 | 元件2 |
| --- | --- |
| 通 | 通 |
| 通 | 断 |
| 断 | 通 |
| 断 | 断 |
共有4种等可能结果,其中至少一个元件通电的结果有3种,
$\therefore P=\frac{3}{4}$
查看更多完整答案,请扫码查看


