16. (10 分) 如图,在⊙O 中,= ,∠C = 75°. 求∠A 的度数.


答案:
∵在⊙O中,AB=AC,
∴∠B=∠C=75°,
∵∠A+∠B+∠C=180°,
∴∠A=180°-∠B-∠C=180°-75°-75°=30°。
答:∠A的度数为30°。
∵在⊙O中,AB=AC,
∴∠B=∠C=75°,
∵∠A+∠B+∠C=180°,
∴∠A=180°-∠B-∠C=180°-75°-75°=30°。
答:∠A的度数为30°。
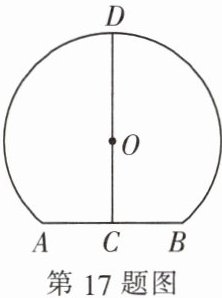
17. (8 分) 如图是一条隧道的横截面,它的形状是以点 O 为圆心的圆的一部分,如果 C 是⊙O 中弦 AB 的中点,CD 经过圆心 O 交⊙O 于点 D,并且 AB = 2,CD = 5. 求⊙O 的半径长.

答案:
设⊙O的半径为$R$,
$\because C$是弦$AB$的中点,$CD$经过圆心$O$,
$\therefore CD \perp AB$,
在$Rt \bigtriangleup ACO$中,$AC = \frac{1}{2}AB = 1$,
$OC = CD - OD = 5 - R$,
根据勾股定理,$AC^{2} + OC^{2} = AO^{2}$,
即$1^{2} + (5 - R)^{2} = R^{2}$,
$1 + 25 - 10R + R^{2} = R^{2}$,
$26 - 10R = 0$,
解得$R = 2.6$。
综上,⊙O的半径长为$2.6$。
$\because C$是弦$AB$的中点,$CD$经过圆心$O$,
$\therefore CD \perp AB$,
在$Rt \bigtriangleup ACO$中,$AC = \frac{1}{2}AB = 1$,
$OC = CD - OD = 5 - R$,
根据勾股定理,$AC^{2} + OC^{2} = AO^{2}$,
即$1^{2} + (5 - R)^{2} = R^{2}$,
$1 + 25 - 10R + R^{2} = R^{2}$,
$26 - 10R = 0$,
解得$R = 2.6$。
综上,⊙O的半径长为$2.6$。
18. (9 分) 如图,在 Rt△ABC 中,∠ACB = 90°,点 O 在边 AC 上,以点 O 为圆心、OC 为半径的半圆与斜边 AB 相切于点 D,交 OA 于点 E,连接 OB.
(1) 求证:BD = BC.
(2) 已知 OC = 1,∠A = 30°,求 AB 的长.
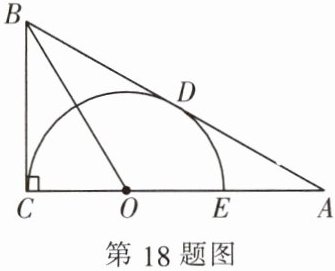
(1) 求证:BD = BC.
(2) 已知 OC = 1,∠A = 30°,求 AB 的长.

答案:
(1) 见解析;
(2) AB=2$\sqrt{3}$.
(1) 见解析;
(2) AB=2$\sqrt{3}$.
查看更多完整答案,请扫码查看


